A uniform. rod of length l can rotate without friction about an axis passing through its upper end (Fig). The rod is deflected by an angle $a_{0}$ and let go. Find the speed of the lower end of the rod as a function of the angle $α$

Text Solution

Verified by Experts

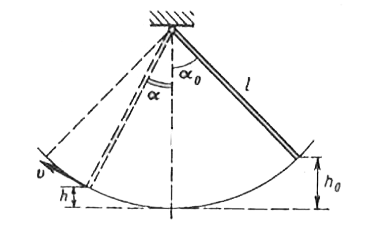
The correct Answer is: $v = \sqrt{3 g l (cos α - {cos α}_{0})}$

Updated on:21/07/2023

A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all points
Bdifferent at differen points and maximum at centre of rod
Cdifferent at different points and minimum at axis of rotation.
Ddifferent at different points and maximum at axis of rotation
The moment of inertia of a uniform rod of length $2 l$ and mass $m$ about an axis $x y$ passing through its centre and inclined at an angle $α$ is

A $\frac{m l^{2}}{3} {sin}^{2} α$
B $\frac{m l^{2}}{12} {sin}^{2} α$
C $\frac{m l^{2}}{2} {cos}^{2} α$
D $\frac{m l^{2}}{2} {cos}^{2} α$
The radius of gyration of an uniform rod of length $l$ about an axis passing through one of its ends and perpendicular to its length is.
A $\frac{l}{\sqrt{2}}$
B $\frac{l}{3}$
C $\frac{l}{\sqrt{3}}$
D $\frac{l}{2}$