Assuming the moment of inertia of the pulley to be I and its radius to be r.
The correct Answer is:u=gm2−m1m1+m2+I/r2
Since the pulley rotates with an acceleration, there must be a torque acting on it due to the difference in the tensions of the left and the right parts of the rope (see Fig) It follows from the fundamental equation of dynamics that
m2g−T2=m2ga,−m1g+T1=m1a,M=IΔω/Δt
The torque is M=(T2−T1)r. The variation of the angular velocity is
Δω=ω2−ω1=v2r−v1r=aΔtr
We m2g−T2=m2a,−m1g+T1=m1a1, T2−T1=Iar2
Hence
a=(m2−m1)gm1+m2+I/r2,T1=2m1m2g(1+I/2m2r2)m1+m2+I/r2
T2=2m1m2g(1+I/2m1r2)m1+m2+I/r2
For I/r2<<m1+m2 we obtain the answer to Problem 3.2

Similar Questions
In the arrangement shown in figure a weight A possesses mass m, a pulley B possesses mass M. Also known are the moment of inertia I of the pulley relative to its axis and the radii of the pulley R and 2R. The mass of the threads is negligible. Find the acceleration of the weight A after the system is set free.

View SolutionThe moment of inertia of a sphere about its diameter is I. Four such spheres are arranged as shown in figure. Find the moment of inertia of the system about the axis XX'. (radius of each sphere is 2R).

View Solution
Knowledge Check
A solid sphere of radius R has moment of inertia l about its diameter. What will be moment of inertia of a shell of same mass and same radius about its diameter?
A35lB53lC23lD25lThe moment of inertia of a uniform cylinder of length landradiusR about its perpendicular bisector is I. What is the ratio l/R such that the moment of inertia is minimum ?
A1B3√2C√32D√32The moment of inertia of a solid sphere of mass M and radius R about its diameter is I. The moment of inertia of the same sphere about a tangent parallel to the diameter is
A5 IB7 IC2.5 ID3.5 I
A solid sphere of mass M and radius R having moment of inertial I about its diameter is recast into a solid disc of radius r and thickness t .The moment of inertia of the disc about an axis passing the edge and perpendicular to the plane remains "I" .Then r=x√15R Find x=?
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
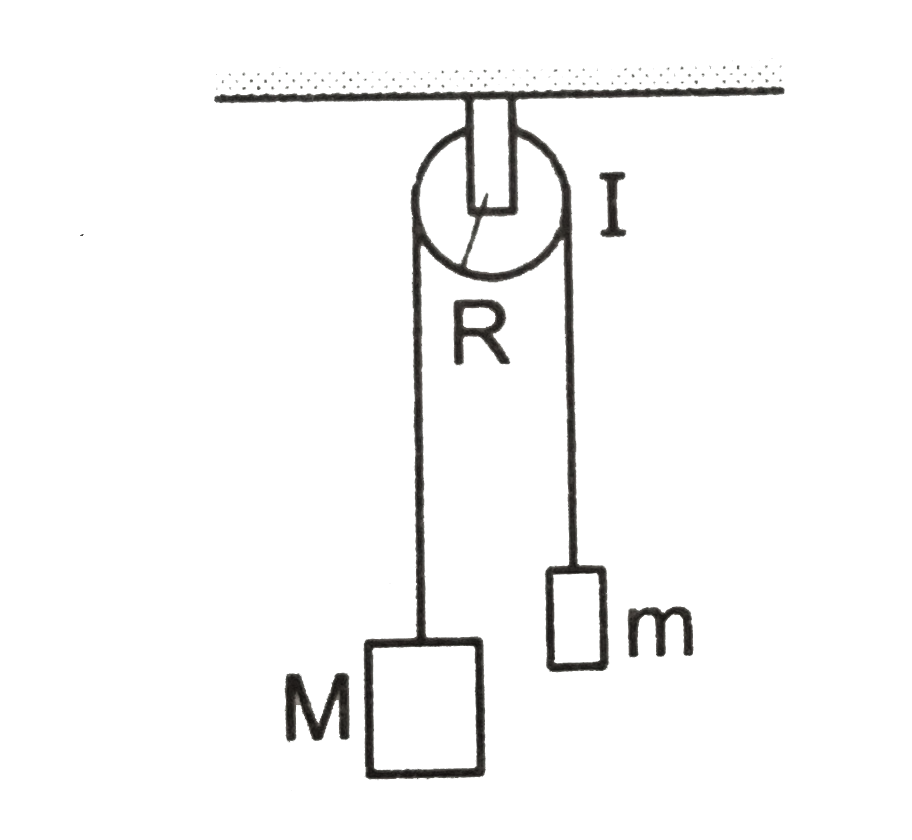
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.

View SolutionThe moment of inertia of a uniform cylinder of length landradiusR about its perpendicular bisector is I. What is the ratio l/R such that the moment of inertia is minimum ?
View SolutionA circular cdotdisc of radius R and thickness R6 has moment of inertia I about the axis perpendicular to the plane and passing through its centre. The disc is melted and recasted into a solid sphere. The moment of inertia of the sphere about its diameter is In. Find n.
View Solution
