The pulleys in filgure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
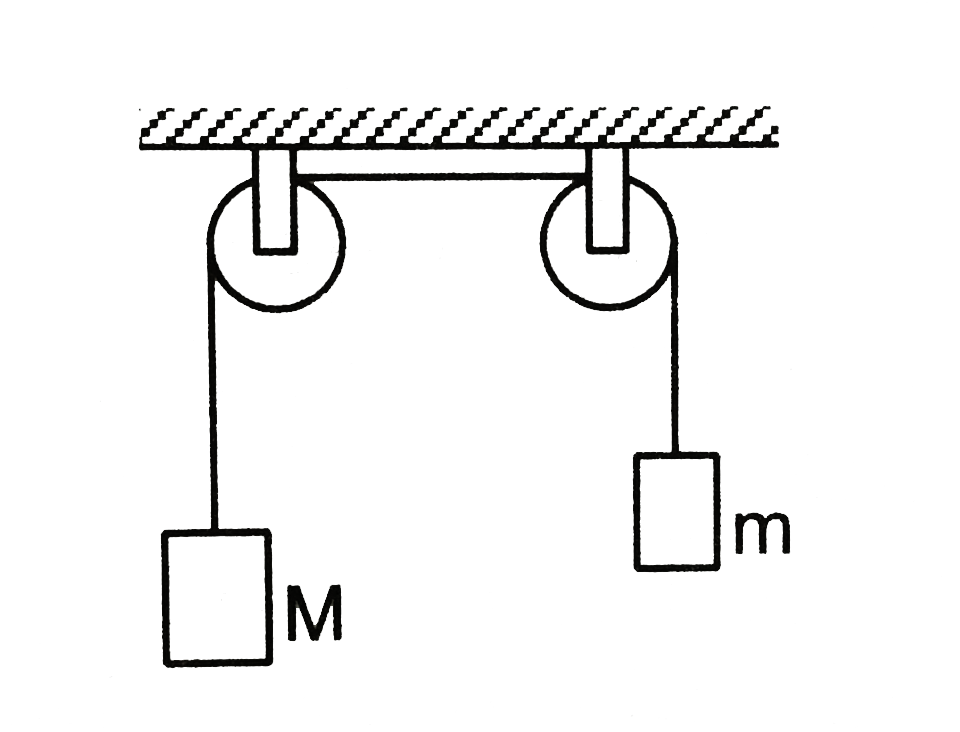
The correct Answer is:B
According to the equation
Mg−T1=Ma….1

(T1−T2)R=IaR
→(T1−T2)=IaR2….. 2
→(T2−T3)R=IaR2……3
→T3−mg=ma…..4
By adding equation 2 and 3 we will get
→(T1−T3)=2IaR2......5
By adding equation 1 and 4 we will get ltbr> −mg+Mg+(T3−T1)=Ma+ma..6
Substitung the value of T3−T1 we will get
→Mg−mg=Ma+ma+2IaR2
→a=(M−m)G(M+m+2IR2)0
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
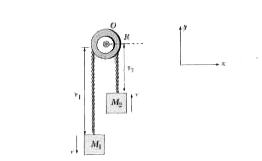
A block of mass M1 and a block of mass M2 are connected by a string that passes over a pulley as shown in Fig. The pulley is a uniform disk of radius R and mass M. Find the acceleration of the two object, using the concepts of angular momentum and torque.
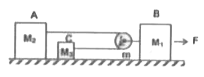
View SolutionThree blocks, placed on smooth horizontal surface are connected by ideal string and a disc shaped pulley of radius r, and mass m. Find the accelerations of the blocks. Masses of the blocks are given as M1=10kg,M2=5kg,M3=2kg,m=2kg.
View Solution
Knowledge Check
A block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
Amg2m+MB2mgm+MCmgm+MD2mg2m+MThe acceleration down the plane of spherical body of mass m radius R and moment of inertia I having inclination θ to the horizontal is
Agsinθ1+12/R2Bgsinθ1+I/R2Cgsinθ1+I/MR2DgsinθMR2+1
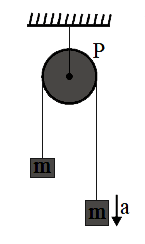
In the figure, the blocks unequal masses m1 and m2 (m1<m2).m2 has a downward acceleration a. The pulley P has a radius r, and some mass. The string does not slip on the pulley. Find the acceleration of block and angular acceleration of pulley. (I = momentum of inerita of pulley)
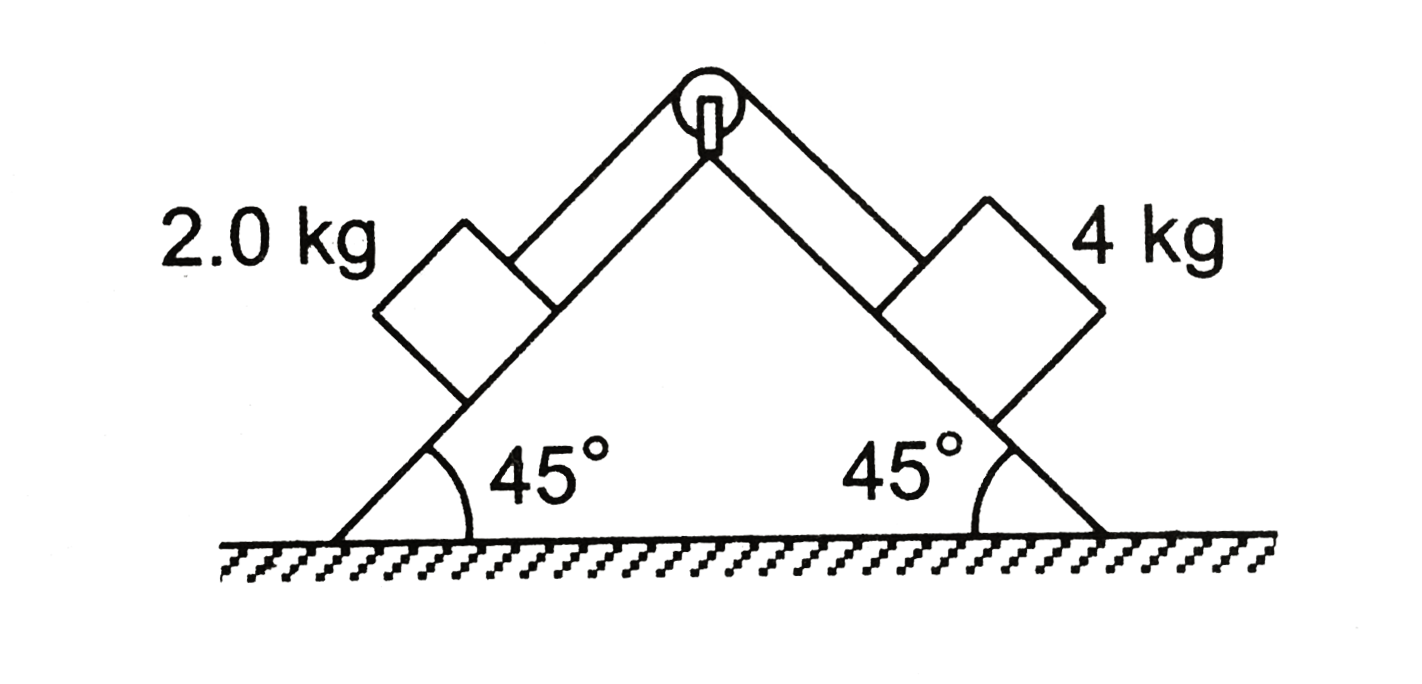
View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
View SolutionThe descending pulley shown in figure has a radius 20 cm and moment of inertia 0.20 kg-m^2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1.0 kg.

View SolutionSuppose the smaller pulley of the previous problem has its radius 5.0 cm and moment of inertia 0.10 kg-m^2. Find the tension in the part of the string joiningk the pulleys.
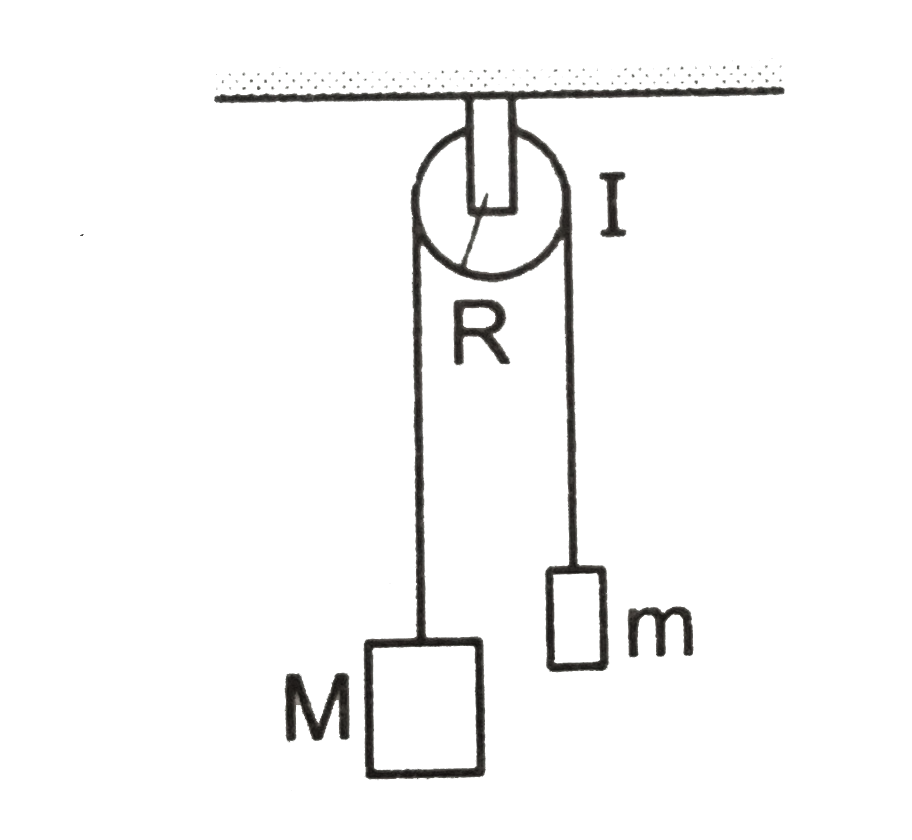
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
View SolutionA small pulley of radius 20 cm and moment of inertia 0.32kg−m2 is used to hang a 2 kg mass with the help of massless string. If the block is released, for no slipping condition find the acceleration of the block ( in m/s2).
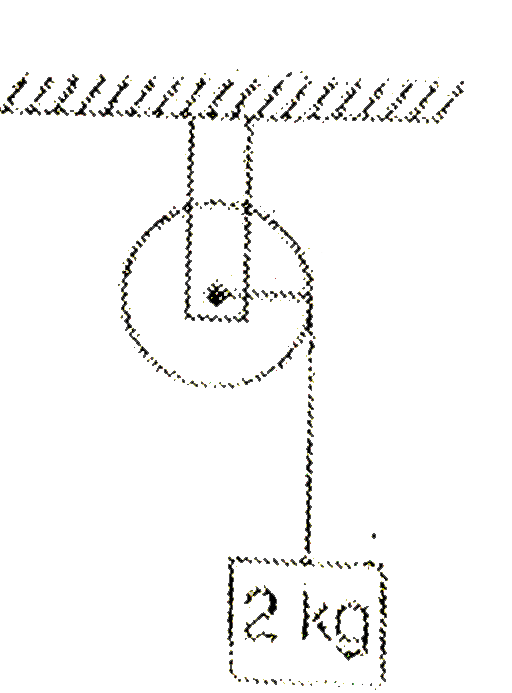
View Solution
