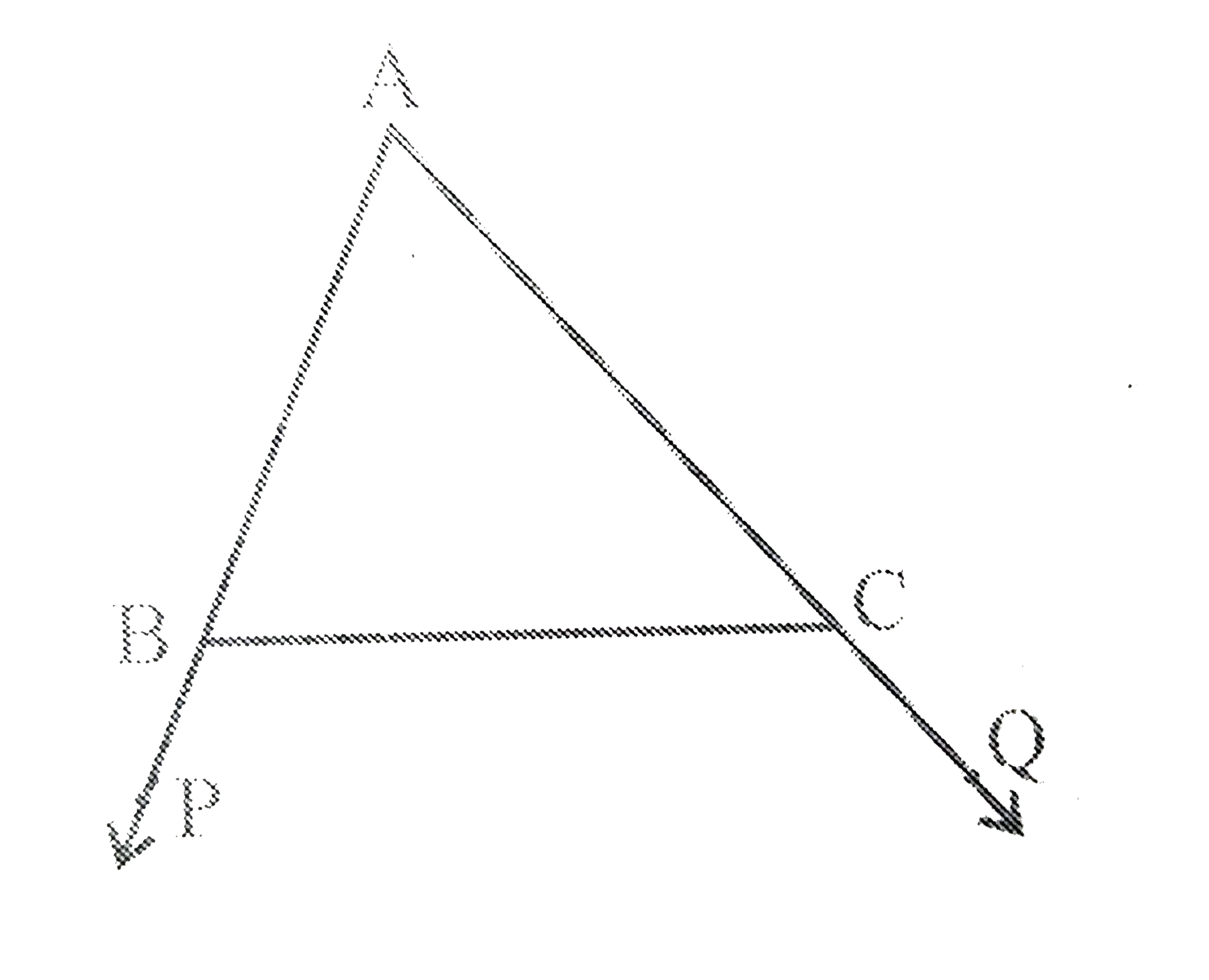
The sides AB and AC of a ABC are produced to P and Q respectively. If the bisectors of ∠PBC AND ∠QCB intersect at O, then ∠boc=900−12∠A GIVEN : A ABC in which sides AB and AC are produced to P and Q respectively. The bisectors of ∠PBC and ∠QCB intersect at O.
Step by step video & image solution for The sides A B and A C of a A B C are produced to P and Q respectively. If the bisectors of /_P B C AND /_Q C B intersect at O , then /_boc=90^0-1/2/_A GIVEN : A A B C in which sides A B and A C are produced to P and Q respectively. The bisectors of /_P B C and /_Q C B intersect at Odot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The sides AB and AC of ABC are product to P and Q respectively. the bisectors of exterior angles at B and C of ABC meet at O (fig.19) prove that ∠BOC=900−12∠A
View SolutionIn Fig. 7.48, sides ABandAC of ΔABC are extended to points PandQ respectively. Also, ∠PBC <∠QCB. Show that AC > AB.
View SolutionIn ABC, if bisectors of ∠ABC and ∠ACB intersect at O at angle of 1200 , then find the measure of ∠A
View SolutionIn a ABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC intersects FE at Q. Prove that AQ=QP.
View SolutionSides BC,CA and BA of a triangle ABC are produced to D,Q,P respectively as shown in Figure. If ∠ACD=1000 and ∠QAP=350, find all the angles of the triangle. Figure
View SolutionSides BC,CA and BA of a triangle ABC are produced to D,Q,P respectively as shown in Figure. If ∠ACD=1000 and ∠QAP=350, find all the angles of the triangle. Figure
View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
View SolutionIn a triangle ABC, ∠ABC= ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC=1200. Show that ∠A=∠B=∠C=600 .
View SolutionIn a triangle ABC,∠ABC=∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC=1200. Show that ∠A=∠B=∠C=600
View SolutionIn a ABC, it is given that AB=AC and the bisectors of ∠B and ∠C intersect at O, If M is a point on BO produced, prove that ∠MOC=∠ABC.
View Solution
