In the adjacent figure ΔABC, ¯¯¯¯¯¯OB,¯¯¯¯¯¯OC are the angle bisectors of ∠B,∠C respectively Intersect at 'O'. ∠BOC=130∘. If ¯¯¯¯¯¯OB=¯¯¯¯¯¯OC , then find ∠A,∠ABC,∠ACB.Solution in Telugu
Step by step video & image solution for In the adjacent figure DeltaABC, bar(OB), bar(OC) are the angle bisectors of angleB, angleC respectively Intersect at 'O'. angleBOC =130^@. If bar(OB)=bar(OC) , then find angleA, angleABC, angleACB. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Which of the following are primaryt and secondary data ?
(i) Collection of the data about enrollment of students in your school for a period from 2001 to 2010.
(ii) Height of students in your class recorded by physical education teacher.
View SolutionTake a cube of edge ‘l' cm. and cut it as we did in the previous activity and find total surface area and lateral surface area of cube.
View SolutionDeltaABC be an equilateral triangle whose orthocentre is the origin 'O' . If bar (OA)=bar a.bar (OB)=bar b then bar (OC) is
View SolutionDeltaABC be an equilateral triangle whose orthocentre is the origin 'O' . If bar (OA)=bar a.bar (OB)=bar b then bar (OC) is
View SolutionOABCD is a pyramid with square base ABCD such that bar(OA),bar(OB),bar(OC),bar(OD) are unit vectors and bar(OA) , bar(OB) = bar(OB) .bar(OC) = bar(OC) . bar(OD) = bar(OD) . bar(OA) =1/2, then volume of the pyramid is
View SolutionIf diagonals of a parallelogram ABCD intersect each other in M, then ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC+¯¯¯¯¯¯OD =
View SolutionLet G be the centroid of a triangle ABC and O be any other point, then ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC is equal to
View SolutionIn a triangle ABC , OB and OC are the bisector of angle ∠B and ∠C respectively . ∠BAC=60∘ . The angle ∠BOC will be :
View SolutionIn the given figure ∠A=40∘. If ¯¯¯¯¯¯BO and ¯¯¯¯¯¯CO are the bisectors of ∠B and ∠C respectively. Find the measure of ∠BOC.
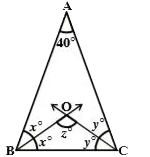
View SolutionIn the given figure ∠A=40∘. If ¯¯¯¯¯¯BO and ¯¯¯¯¯¯CO are the bisectors of ∠B and ∠C respectively. Find the measure of ∠BOC.
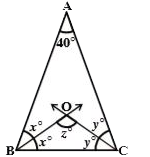
View SolutionIn the given figure ∠A=40∘. If ¯¯¯¯¯¯BO and ¯¯¯¯¯¯CO are the bisectors of ∠B and ∠C respectively. Find the measure of ∠BOC.
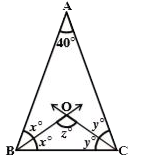
View SolutionIn the given figure ∠A=40∘. If ¯¯¯¯¯¯BO and ¯¯¯¯¯¯CO are the bisectors of ∠B and ∠C respectively. Find the measure of ∠BOC.

View SolutionIf O is the circumcentre, 'H' is the orthocentre of triangle ABC, then show that
¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC=¯¯¯¯¯¯OH
View SolutionIf S is the circumcentre, O is the orthocentre of Δ ABC then →OA+→OB+→OC=
View SolutionΔABC be an equilateral triangle whose orthocentre is the origin 'O'. If ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b then ¯¯¯¯¯¯OC is
View SolutionIf OABC, OCDE, OEFA are adjacent faces of a cube OABCDEF then ¯¯¯¯¯¯OB+¯¯¯¯¯¯OD+¯¯¯¯¯¯OF interms of ¯¯¯¯¯¯OA,¯¯¯¯¯¯OE,¯¯¯¯¯¯OC is
View Solution
