Find the area of the largest rectangle in the first quadrant with two sides on x-axis and y-axis and one vertex on the curve y=12−x2
The correct Answer is:16cm2
To find the area of the largest rectangle in the first quadrant with two sides on the x-axis and y-axis and one vertex on the curve y=12−x2, we can follow these steps:
Step 1: Understand the problem
We need to find a rectangle in the first quadrant where one vertex lies on the curve y=12−x2. The rectangle will have its base along the x-axis and its height along the y-axis.
Step 2: Define the rectangle's dimensions
Let the vertex of the rectangle on the curve be at the point (x,y). The rectangle will then have:
- Length = x (along the x-axis)
- Height = y (along the y-axis)
Step 3: Express the area of the rectangle
The area A of the rectangle can be expressed as:
A=Length×Height=x×y
Since the vertex lies on the curve, we can substitute y with 12−x2:
A=x(12−x2)=12x−x3
Step 4: Differentiate the area function
To find the maximum area, we need to differentiate the area function A with respect to x:
dAdx=12−3x2
Step 5: Set the derivative to zero
To find the critical points, set the derivative equal to zero:
12−3x2=0
Solving for x:
3x2=12⟹x2=4⟹x=±2
Since we are in the first quadrant, we take x=2.
Step 6: Find the corresponding y
Now, substitute x=2 back into the equation for y:
y=12−x2=12−22=12−4=8
Step 7: Calculate the area
Now we can calculate the area of the rectangle:
A=x×y=2×8=16
Conclusion
The area of the largest rectangle is 16 square units.
We need to find a rectangle in the first quadrant where one vertex lies on the curve y=12−x2. The rectangle will have its base along the x-axis and its height along the y-axis.
Let the vertex of the rectangle on the curve be at the point (x,y). The rectangle will then have:
- Length = x (along the x-axis)
- Height = y (along the y-axis)
The area A of the rectangle can be expressed as:
A=Length×Height=x×y
Since the vertex lies on the curve, we can substitute y with 12−x2:
A=x(12−x2)=12x−x3
To find the maximum area, we need to differentiate the area function A with respect to x:
dAdx=12−3x2
To find the critical points, set the derivative equal to zero:
12−3x2=0
Solving for x:
3x2=12⟹x2=4⟹x=±2
Since we are in the first quadrant, we take x=2.
Now, substitute x=2 back into the equation for y:
y=12−x2=12−22=12−4=8
Now we can calculate the area of the rectangle:
A=x×y=2×8=16
The area of the largest rectangle is 16 square units.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - MODEL TEST PAPER - 4EXERCISE - SECTION - B10videos
MODEL TEST PAPER - 4
- BOOK - ICSECHAPTER - MODEL TEST PAPER - 4EXERCISE - SECTION - C10videos
MODEL TEST PAPER - 4
- BOOK - ICSECHAPTER - MODEL TEST PAPER - 3 EXERCISE - SECTION - C10videos
MODEL TEST PAPER - 3
- BOOK - ICSECHAPTER - MODEL TEST PAPER - 7EXERCISE - Section - C5videos
MODEL TEST PAPER - 7
Similar Questions
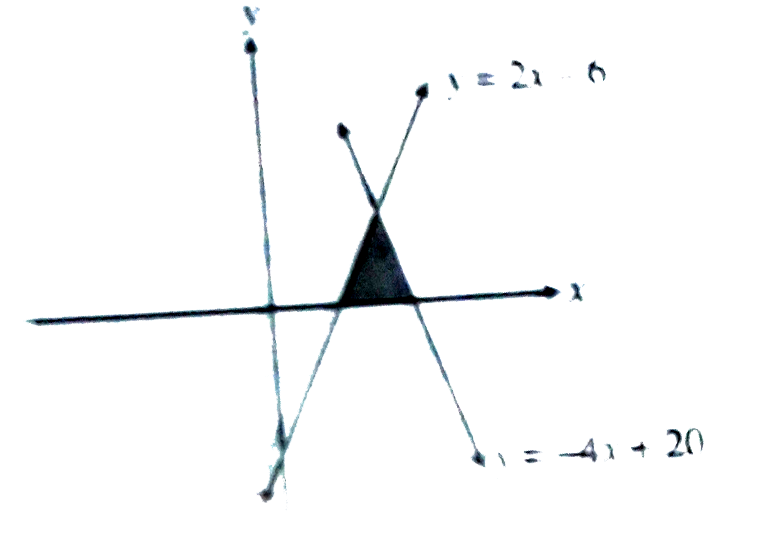
Find the area of the triangle that lies in the first quadrant , with its base on the x-axis and that is bounded by the lines y=2x-6 and y=-4x+20 (the shaded area in the diagram shown above).View SolutionFind the area of the region in the first quadrant enclosed by x-axis, line x=√3yand the circle x2+y2=4.
View SolutionWrite the co-ordinates of the vertices of a rectangle which is 6 units long and 4 units wide. If the rectangle is in the first quadrant. Its longer side lies on x-axis and oner vertex is at the origin.
View SolutionFind the area of the largest rectangle with lower base on the x-axis and upper vertices on the curve y=12−x2.
View SolutionThe largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
View SolutionFind the area bounded by the curve y=√x,x=2y+3 in the first quadrant and X-axis.
View SolutionFind the area of the region bounded by y=√x, x=2y+3 in the first quadrant and x-axis.
View SolutionFind the area of the region in the first quadrant enclosed by x-axis, the line y=√3 x and the circle x2+y2=16
View SolutionFind the area of the region in the first quadrant enclosed by the x-axis, the line y = x , and the circle x2+y2=32 .
View SolutionFind the area of the figure lying in the first quadrant and bounded by the curves y2=4x,x2=4y.
View Solution

