In a ΔABC,AD:DB=1:3,AE:EC=2:3,BF:FC=1:2. Find the ratio of area of Δ of ΔDEF:ΔABC.
The correct Answer is:14
To find the ratio of the area of triangle DEF to triangle ABC given the ratios of segments AD:DB, AE:EC, and BF:FC, we will follow these steps:
Step 1: Understand the Ratios
We have the following ratios:
- AD:DB=1:3
- AE:EC=2:3
- BF:FC=1:2
Step 2: Assign Lengths to Segments
Let:
- AD=1x and DB=3x (thus, AB=AD+DB=4x)
- AE=2y and EC=3y (thus, AC=AE+EC=5y)
- BF=1z and FC=2z (thus, BC=BF+FC=3z)
Step 3: Calculate the Area of Triangle ABC
The area of triangle ABC can be calculated using the formula:
AreaABC=12×AB×AC×sin(B)
Substituting the lengths:
AreaABC=12×(4x)×(5y)×sin(B)=10xysin(B)
Step 4: Calculate the Area of Triangle DEF
To find the area of triangle DEF, we will use the ratios of the segments to find the areas of triangles ADB, AEC, and BFC.
1. Area of Triangle ADB:
AreaADB=12×AD×AB×sin(B)=12×(1x)×(4x)×sin(B)=2x2sin(B)
2. Area of Triangle AEC:
AreaAEC=12×AE×AC×sin(B)=12×(2y)×(5y)×sin(B)=5y2sin(B)
3. Area of Triangle BFC:
AreaBFC=12×BF×BC×sin(B)=12×(1z)×(3z)×sin(B)=32z2sin(B)
Step 5: Calculate the Area of Triangle DEF
The area of triangle DEF can be found by subtracting the areas of triangles ADB, AEC, and BFC from the area of triangle ABC:
AreaDEF=AreaABC−(AreaADB+AreaAEC+AreaBFC)
Substituting the areas:
AreaDEF=10xysin(B)−(2x2sin(B)+5y2sin(B)+32z2sin(B))
Factoring out sin(B):
AreaDEF=sin(B)(10xy−(2x2+5y2+32z2))
Step 6: Find the Ratio of Areas
Now, we can find the ratio of the areas:
Ratio=AreaDEFAreaABC=sin(B)(10xy−(2x2+5y2+32z2))10xysin(B)
Cancelling sin(B):
Ratio=10xy−(2x2+5y2+32z2)10xy
Final Ratio
To get the final ratio, we need to evaluate the expression based on the values of x, y, and z. However, we can conclude that the ratio of the areas of triangle DEF to triangle ABC is a function of the segments defined by the ratios provided.
We have the following ratios:
- AD:DB=1:3
- AE:EC=2:3
- BF:FC=1:2
Let:
- AD=1x and DB=3x (thus, AB=AD+DB=4x)
- AE=2y and EC=3y (thus, AC=AE+EC=5y)
- BF=1z and FC=2z (thus, BC=BF+FC=3z)
The area of triangle ABC can be calculated using the formula:
AreaABC=12×AB×AC×sin(B)
Substituting the lengths:
AreaABC=12×(4x)×(5y)×sin(B)=10xysin(B)
To find the area of triangle DEF, we will use the ratios of the segments to find the areas of triangles ADB, AEC, and BFC.
AreaADB=12×AD×AB×sin(B)=12×(1x)×(4x)×sin(B)=2x2sin(B)
AreaAEC=12×AE×AC×sin(B)=12×(2y)×(5y)×sin(B)=5y2sin(B)
AreaBFC=12×BF×BC×sin(B)=12×(1z)×(3z)×sin(B)=32z2sin(B)
The area of triangle DEF can be found by subtracting the areas of triangles ADB, AEC, and BFC from the area of triangle ABC:
AreaDEF=AreaABC−(AreaADB+AreaAEC+AreaBFC)
Substituting the areas:
AreaDEF=10xysin(B)−(2x2sin(B)+5y2sin(B)+32z2sin(B))
Factoring out sin(B):
AreaDEF=sin(B)(10xy−(2x2+5y2+32z2))
Now, we can find the ratio of the areas:
Ratio=AreaDEFAreaABC=sin(B)(10xy−(2x2+5y2+32z2))10xysin(B)
Cancelling sin(B):
Ratio=10xy−(2x2+5y2+32z2)10xy
To get the final ratio, we need to evaluate the expression based on the values of x, y, and z. However, we can conclude that the ratio of the areas of triangle DEF to triangle ABC is a function of the segments defined by the ratios provided.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If ΔABC~ΔDEF such that AB=1.2 cm and DE =1.4 cm, the ratio of the areas of ΔABC and ΔDEF is :
A49:36B6:7C7:6D36:49
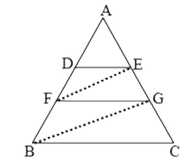
In a ΔABC,DE||EG||BCandEF∣∣BG and D is a midpoint of AF. Find the ratio of area of ΔDEF:ΔABC
View SolutionΔABC is right-angled at A and AD⊥BC. If BC=13cmandAC=5cm, find the ratio of areas of ΔABCandΔADC.

View SolutionIn a triangle ABC , D & E are two points on sides AB and AC such that DE∣∣BC and AD:DB=3:5. Find the ratio of area of ΔADE to the area of trapezium BDEC.
View SolutionIn ΔABCAD divides BC in 1 : 3 find the ratio of triangle ADB and ADC ?
View SolutionIn a triangle ABC, median BE and CF intersect at O. Find the ratio of area of ΔOFEandΔABC.
View SolutionIn ΔABC,DandE are the midpoint of AB and AC respectively. Find the ratio of the areas of ΔADEandΔABC.

View SolutionIn a triangle ABC, there are three point P, Q & R on side BC, such that BP:PQ:QR:RC=1:2:3:4 . If G is the centroid, then find the ratio of area of ΔPGR to area ΔABC.
View Solution

