When 335 is added to 5A7, the result is 8B2. 8B2 is divisible by 3. What is the largest possible value of A?
8
2
1
4
The correct Answer is:D
To solve the problem step by step, we will follow the instructions provided in the video transcript while ensuring clarity in each step.
Step 1: Set Up the Equation
We know that when 335 is added to 5A7, the result is 8B2. We can express this mathematically as:
5A7+335=8B2
Step 2: Perform the Addition
Let's add the numbers:
- The units place: 7+5=12 (write down 2 and carry over 1)
- The tens place: A+3+1=A+4
- The hundreds place: 5+3=8
Thus, we have:
8B2 where B=A+4
Step 3: Determine the Values of B
Since 8B2 must be divisible by 3, we need to find the sum of its digits:
8+B+2=10+B
This sum must be divisible by 3.
Step 4: Find Possible Values for B
Now we will check for values of B (which is a digit from 0 to 9) that make 10+B divisible by 3:
- If B=0: 10+0=10 (not divisible by 3)
- If B=1: 10+1=11 (not divisible by 3)
- If B=2: 10+2=12 (divisible by 3)
- If B=3: 10+3=13 (not divisible by 3)
- If B=4: 10+4=14 (not divisible by 3)
- If B=5: 10+5=15 (divisible by 3)
- If B=6: 10+6=16 (not divisible by 3)
- If B=7: 10+7=17 (not divisible by 3)
- If B=8: 10+8=18 (divisible by 3)
- If B=9: 10+9=19 (not divisible by 3)
The possible values for B are 2, 5, and 8.
Step 5: Calculate Corresponding Values for A
Now we will find the corresponding values of A for each valid B:
1. If B=2:
A+4=2
A=2−4=−2 (not valid)
2. If B=5:
A+4=5
A=5−4=1 (valid)
3. If B=8:
A+4=8
A=8−4=4 (valid)
Step 6: Determine the Largest Possible Value of A
The valid values of A from our calculations are 1 and 4. The largest possible value of A is:
Largest possible value of A=4
Final Answer
The largest possible value of A is 4.
---
We know that when 335 is added to 5A7, the result is 8B2. We can express this mathematically as:
5A7+335=8B2
Let's add the numbers:
- The units place: 7+5=12 (write down 2 and carry over 1)
- The tens place: A+3+1=A+4
- The hundreds place: 5+3=8
8B2 where B=A+4
Since 8B2 must be divisible by 3, we need to find the sum of its digits:
8+B+2=10+B
This sum must be divisible by 3.
Now we will check for values of B (which is a digit from 0 to 9) that make 10+B divisible by 3:
- If B=0: 10+0=10 (not divisible by 3)
- If B=1: 10+1=11 (not divisible by 3)
- If B=2: 10+2=12 (divisible by 3)
- If B=3: 10+3=13 (not divisible by 3)
- If B=4: 10+4=14 (not divisible by 3)
- If B=5: 10+5=15 (divisible by 3)
- If B=6: 10+6=16 (not divisible by 3)
- If B=7: 10+7=17 (not divisible by 3)
- If B=8: 10+8=18 (divisible by 3)
- If B=9: 10+9=19 (not divisible by 3)
Now we will find the corresponding values of A for each valid B:
1. If B=2:
A+4=2
A=2−4=−2 (not valid)
A+4=5
A=5−4=1 (valid)
A+4=8
A=8−4=4 (valid)
The valid values of A from our calculations are 1 and 4. The largest possible value of A is:
Largest possible value of A=4
The largest possible value of A is 4.
Topper's Solved these Questions
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - NUMBER SYSTEM EXERCISE - MULTIPLE CHOICE QUESTIONS225videos
NUMBER SYSTEM
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - MOCK TEST IIEXERCISE - MCQ100videos
MOCK TEST II
- BOOK - ADVANCED MATHS BY ABHINAY MATHS ENGLISHCHAPTER - PARTNERSHIPEXERCISE - Questions26videos
PARTNERSHIP
Similar Questions
Knowledge Check
- Question 1 - Select One
If the mode of 2.5, 2.7, 2.8, 2.7, 2.5, x , 2.8, 2.7, 2.8 is 2.8, then what is the value of x?
A2.1B2.5C2.7D2.8 - Question 2 - Select One
Digits 2, 3, 4, 6, 7, 8 are arranged in the following blanks :
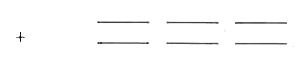
The largest possible number after addition isA1308B808C1605D1560
32n+7 is divisible by (A) 8 (B) 4 (C) 16
View SolutionWhat should be added to 7415— to get 825— ?
View SolutionA number is doubled and 9 s added. If the resultant is trebled, it becomes 75. What is that number? a. 3.5 b. 6 c. 8 d. none of these
View SolutionWhat is the value of 817+537+427+317
View SolutionIf the number A 3 6 4 0 5 4 8 9 8 1 2 7 0 6 4 4 B is divisible by 99 then the ordered pair of digits (A, B) is
View SolutionIf a−b=2 and ab=8, then what is the value of a3−b3?
View Solution

