Question

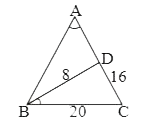
ABC is a $\Delta$ BD = 8 BC = 20 CD = 16 $\angle CBD=\angle CAB$ find perimeter of ABC

Answer

`44 cm `

Explanation

To find the perimeter of triangle ABC given the conditions in the problem, we can follow these steps:

Step 1: Understand the Triangle Configuration
We have triangle ABC with point D on side AC. The lengths are given as:
- BD = 8
- BC = 20
- CD = 16
- Angle CBD = Angle CAB

Step 2: Set Up the Relationship Using Congruence
Since angle CBD is equal to angle CAB, triangles ABD and BDC are similar by the Angle-Angle (AA) criterion. This means:
\( \frac{AB}{BC} = \frac{BD}{CD} \)

Step 3: Substitute Known Values
Now, substituting the known values into the proportion:
- AB = ?
- BC = 20
- BD = 8
- CD = 16

The equation becomes:
\( \frac{AB}{20} = \frac{8}{16} \)

Step 4: Simplify the Ratio
Simplifying the right side:
\( \frac{8}{16} = \frac{1}{2} \)
So the equation now looks like:
\( \frac{AB}{20} = \frac{1}{2} \)

Step 5: Solve for AB
Cross-multiplying gives:
\( AB = 20 \times \frac{1}{2} = 10 \)

Step 6: Find AC
Next, we can find AC using the relationship in triangle BDC:
Since BD + CD = AC,
\( AC = BD + CD = 8 + 16 = 24 \)

Step 7: Calculate the Perimeter
Now we can find the perimeter of triangle ABC:
\( \text{Perimeter} = AB + BC + AC \)
Substituting the known values:
\( \text{Perimeter} = 10 + 20 + 24 = 54 \)

Final Answer
The perimeter of triangle ABC is 54.

---