ABCD is a quadrilateral with AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and angle ABC is a right-angle.
What is the difference between perimeter of triangle ABC and perimeter of triangle ADC ?
4 cm
5 cm
6 cm
7 cm
To solve the problem, we need to find the difference between the perimeters of triangles ABC and ADC in the quadrilateral ABCD.
1. Identify the given dimensions:
- AB = 9 cm
- BC = 40 cm
- CD = 28 cm
- DA = 15 cm
- Angle ABC = 90 degrees
2. Draw the quadrilateral ABCD:
- Draw a right triangle ABC with AB and BC as the two legs.
- Label the points A, B, C, and D appropriately.
3. Calculate the length of AC using the Pythagorean theorem:
- Since triangle ABC is a right triangle, we can use the Pythagorean theorem:
AC2=AB2+BC2
- Substituting the values:
AC2=92+402=81+1600=1681
- Therefore, AC=√1681=41 cm.
4. Calculate the perimeter of triangle ABC:
- The perimeter of triangle ABC is:
PABC=AB+BC+AC=9+40+41=90 cm
5. Calculate the perimeter of triangle ADC:
- The perimeter of triangle ADC is:
PADC=DA+CD+AC=15+28+41=84 cm
6. Find the difference between the perimeters:
- The difference between the perimeter of triangle ABC and triangle ADC is:
Difference=PABC−PADC=90−84=6 cm
Final Answer:
The difference between the perimeter of triangle ABC and the perimeter of triangle ADC is 6 cm.
- AB = 9 cm
- BC = 40 cm
- CD = 28 cm
- DA = 15 cm
- Angle ABC = 90 degrees
- Draw a right triangle ABC with AB and BC as the two legs.
- Label the points A, B, C, and D appropriately.
- Since triangle ABC is a right triangle, we can use the Pythagorean theorem:
AC2=AB2+BC2
- Substituting the values:
AC2=92+402=81+1600=1681
- Therefore, AC=√1681=41 cm.
- The perimeter of triangle ABC is:
PABC=AB+BC+AC=9+40+41=90 cm
- The perimeter of triangle ADC is:
PADC=DA+CD+AC=15+28+41=84 cm
- The difference between the perimeter of triangle ABC and triangle ADC is:
Difference=PABC−PADC=90−84=6 cm
The difference between the perimeter of triangle ABC and the perimeter of triangle ADC is 6 cm.
Similar Questions
Knowledge Check
In ΔABC, AB=6√3cm, AC=12cm and BC=6cm. Then ∠B is
A45∘B60∘C90∘D120∘
In a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral.
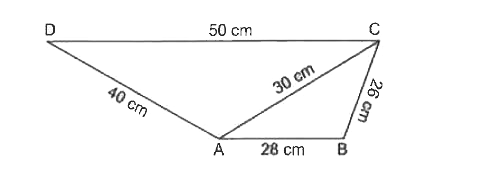
View SolutionFind the area of the quadrilateral ABCD, in which AB=7cm, BC=6cm, CD=12 cm, DA=15cm and AC=9 cm.
View SolutionFind the area of the quadrilateral ABCD , in which AB=7cm,BC=6cm,CD=12cm,DA=15cmandAC=9cm
View SolutionFind the area of the quadrilateral ABCD; in which AB = 7 cm; BC =6 cm;CD =12 cm; DA= 15 cm and AC =9 cm
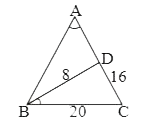
View SolutionIn this ΔABC,BD=8cm,BC=20cm,CD=16cmand∠CBD=∠CAB. Find the perimeter of ΔBDA.
View SolutionIf triangle ABC is similar to triangle PQR , Perimeter of triangle ABC = 30 cm , Perimeter of triangle = 45 cm , PR = 9 cm then find AC.
View SolutionABC is a triangle and D is a point on the side BC. If BC = 12 cm, BD = 9 cm and ∠ADC=∠BAC, then the length of AC is equal to
View Solution
