If area of regular octagon is 18(√2+1) . Find this side
The correct Answer is:a=3
To find the side length of a regular octagon given its area, we can use the formula for the area of a regular octagon:
Area=2a2(√2+1)
where a is the length of a side of the octagon.
Given that the area is 18(√2+1), we can set up the equation:
2a2(√2+1)=18(√2+1)
Step 1: Simplify the equation
Since both sides of the equation have the term √2+1, we can divide both sides by √2+1 (assuming √2+1≠0):
2a2=18
Step 2: Solve for a2
Now, we can solve for a2 by dividing both sides by 2:
a2=182=9
Step 3: Solve for a
Now we take the square root of both sides to find a:
a=√9=3
Thus, the side length of the regular octagon is:
3
Since both sides of the equation have the term √2+1, we can divide both sides by √2+1 (assuming √2+1≠0):
Now, we can solve for a2 by dividing both sides by 2:
Now we take the square root of both sides to find a:
Topper's Solved these Questions
Similar Questions
The area of a regular octagon of side length a is A.
(a) Find the time rate of change of area of the octagon if its side length is being increased at a constant rate of βm/s. Is the time rate of change of area of the octagon constant with time ?
(b) Find the approximate change in area of the octagon as the side length is increased from 2.0 m to 2.001 m.
View SolutionIn the given figure a quadrilateral is formed by joining the alternate vertices of a regular octagon. If the area of the octagon be 2(√2−1)sq cm, find the area of the square.

View Solution
Knowledge Check
The area of a regular hexagon of side 2√3 cm is
A18√3cm2B12√3cm2C36√3cm2D27√3cm2The area of a regular hexagon of side 2√3 cm is :
A18√3cm2B12√3cm2C36√3cm2D27√3cm2The area of an equilateral triangle is 18√3 sq. units. Find the value of side (in units) of the tri angle.
A√2B2√2C3√2D6√2
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
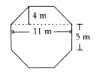
View SolutionThe area of a regular hexagon of side 2√3 cm is :
View SolutionPerimeter of regular octagon is ________ .
View SolutionIf every interior angle of regular octagon is 135∘, then find the external angle of it.
View SolutionArea of regular hexagon with side 'a' is
View Solution
