Derive an expression per the M.I. of a rectangular rod about an axis passing through its centre of mass and perpendicular to its length.
To derive the expression for the moment of inertia (M.I.) of a rectangular rod about an axis passing through its center of mass and perpendicular to its length, we can follow these steps:
Step 1: Define the dimensions of the rectangular rod
Let the length of the rectangular rod be a and the width (or breadth) be b. The mass of the rod is m.
Step 2: Identify the axes of rotation
We will consider the axis of rotation to be the x-axis, which passes through the center of mass of the rod and is perpendicular to its length.
Step 3: Use the formula for the moment of inertia
The moment of inertia Ix about the x-axis for a rectangular rod can be derived using the formula:
Ix=∫r2dm
where r is the distance from the axis of rotation to the mass element dm.
Step 4: Set up the integral
For a rectangular rod, we can consider it to be composed of infinitesimally thin strips of width dy along its length. The distance r from the x-axis for a strip located at a distance y from the center is y. The mass element dm can be expressed as:
dm=mady
where ma is the mass per unit length.
Step 5: Determine the limits of integration
The limits of integration for y will be from −b2 to b2 since the width of the rod extends symmetrically about the center.
Step 6: Evaluate the integral
Now, substituting dm and r into the integral:
Ix=∫b2−b2y2(mady)
This simplifies to:
Ix=ma∫b2−b2y2dy
Calculating the integral:
∫y2dy=y33
Evaluating from −b2 to b2:
(y33)b2−b2=(b2)33−⎛⎝−(b2)33⎞⎠=2⋅b383=b312
Thus, we have:
Ix=ma⋅b312=mb312a
Step 7: Apply the perpendicular axis theorem
According to the perpendicular axis theorem, for a planar object, the moment of inertia about an axis perpendicular to the plane (z-axis) is given by:
Iz=Ix+Iy
Where Iy is the moment of inertia about the y-axis. For the y-axis, we can similarly derive:
Iy=ma312b
Step 8: Combine the results
Thus, the moment of inertia about the z-axis is:
Iz=Ix+Iy=mb312+ma312=m(a2+b2)12
Final Expression
The final expression for the moment of inertia of a rectangular rod about an axis passing through its center of mass and perpendicular to its length is:
Iz=m(a2+b2)12
Let the length of the rectangular rod be a and the width (or breadth) be b. The mass of the rod is m.
We will consider the axis of rotation to be the x-axis, which passes through the center of mass of the rod and is perpendicular to its length.
The moment of inertia Ix about the x-axis for a rectangular rod can be derived using the formula:
Ix=∫r2dm
where r is the distance from the axis of rotation to the mass element dm.
For a rectangular rod, we can consider it to be composed of infinitesimally thin strips of width dy along its length. The distance r from the x-axis for a strip located at a distance y from the center is y. The mass element dm can be expressed as:
dm=mady
where ma is the mass per unit length.
The limits of integration for y will be from −b2 to b2 since the width of the rod extends symmetrically about the center.
Now, substituting dm and r into the integral:
Ix=∫b2−b2y2(mady)
This simplifies to:
Ix=ma∫b2−b2y2dy
Calculating the integral:
∫y2dy=y33
Evaluating from −b2 to b2:
(y33)b2−b2=(b2)33−⎛⎝−(b2)33⎞⎠=2⋅b383=b312
Thus, we have:
Ix=ma⋅b312=mb312a
According to the perpendicular axis theorem, for a planar object, the moment of inertia about an axis perpendicular to the plane (z-axis) is given by:
Iz=Ix+Iy
Where Iy is the moment of inertia about the y-axis. For the y-axis, we can similarly derive:
Iy=ma312b
Thus, the moment of inertia about the z-axis is:
Iz=Ix+Iy=mb312+ma312=m(a2+b2)12
The final expression for the moment of inertia of a rectangular rod about an axis passing through its center of mass and perpendicular to its length is:
Iz=m(a2+b2)12
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (SHORT ANSWER QUESTIONS)
35 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (VERY SHORT ANSWER QUESTIONS)
14 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS)
14 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
Derive an expression for the MI. of a disc,
(i) about an axis passing through its centre and perpendicular to its plane. (ii) about its diameter.
View SolutionThe mass of a unifprm rod is 0.4 kg and its length is 2 m. .Calculate the radius of gyration of the rod about an axis passing through its centre of mass and perpendicular to its length ?
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View SolutionA thin uniform rod 0.75 m long and having a mass 1.5 kg rotates 7 times per second about an axis passing through its centre of gravity and perpendicular to its length. Find its kinetic energy ?
View SolutionTwo thin uniform rods A (M.L) and B (3M,3L) are joined as shown. Find the M.I. about an axis passing through the center of mass of system of rods and perpendicular to the length.

View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
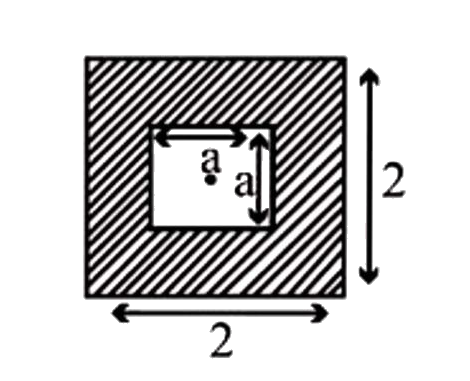
View Solution
