Derive an equation for the angle covered by, a rotating rigid body in the nth second.
To derive the equation for the angle covered by a rotating rigid body in the nth second, we will follow these steps:
Step 1: Understand the Concept
The angle covered in the nth second can be defined as the difference between the angular displacement at the end of n seconds and the angular displacement at the end of (n-1) seconds.
Step 2: Write the Formula for Angular Displacement
The angular displacement θ at any time t is given by the equation:
θ=ω0t+12αt2
where:
- θ is the angular displacement,
- ω0 is the initial angular velocity,
- α is the angular acceleration,
- t is the time.
Step 3: Calculate Angular Displacement at n Seconds
Using the formula, the angular displacement at n seconds is:
θn=ω0n+12αn2
Step 4: Calculate Angular Displacement at (n-1) Seconds
Similarly, the angular displacement at (n−1) seconds is:
θn−1=ω0(n−1)+12α(n−1)2
Step 5: Find the Angle Covered in the nth Second
The angle covered in the nth second, θ(nth)n, is given by:
θ(nth)n=θn−θn−1
Substituting the values from Steps 3 and 4:
θ(nth)n=(ω0n+12αn2)−(ω0(n−1)+12α(n−1)2)
Step 6: Simplify the Expression
Expanding the equation:
θ(nth)n=ω0n+12αn2−(ω0n−ω0+12α(n2−2n+1))
This simplifies to:
θ(nth)n=ω0+12αn2−12α(n2−2n+1)
=ω0+12αn2−12αn2+αn−12α
=ω0+αn−12α
Step 7: Final Equation
Thus, we can express the angle covered in the nth second as:
θ(nth)n=ω0+12α(2n−1)
Final Result
The equation for the angle covered by a rotating rigid body in the nth second is:
θ(nth)n=ω0+12α(2n−1)
---
The angle covered in the nth second can be defined as the difference between the angular displacement at the end of n seconds and the angular displacement at the end of (n-1) seconds.
The angular displacement θ at any time t is given by the equation:
θ=ω0t+12αt2
where:
- θ is the angular displacement,
- ω0 is the initial angular velocity,
- α is the angular acceleration,
- t is the time.
Using the formula, the angular displacement at n seconds is:
θn=ω0n+12αn2
Similarly, the angular displacement at (n−1) seconds is:
θn−1=ω0(n−1)+12α(n−1)2
The angle covered in the nth second, θ(nth)n, is given by:
θ(nth)n=θn−θn−1
Substituting the values from Steps 3 and 4:
θ(nth)n=(ω0n+12αn2)−(ω0(n−1)+12α(n−1)2)
Expanding the equation:
θ(nth)n=ω0n+12αn2−(ω0n−ω0+12α(n2−2n+1))
This simplifies to:
θ(nth)n=ω0+12αn2−12α(n2−2n+1)
=ω0+12αn2−12αn2+αn−12α
=ω0+αn−12α
Thus, we can express the angle covered in the nth second as:
θ(nth)n=ω0+12α(2n−1)
The equation for the angle covered by a rotating rigid body in the nth second is:
θ(nth)n=ω0+12α(2n−1)
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (VERY SHORT ANSWER QUESTIONS)
14 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM EQUATIONS OF ROTATIONAL MOTION)
8 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (LONG ANSWER QUESTIONS)
14 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
Knowledge Check
For a perfectly rigid body
AYoung's modulus is infinite and bulk modulus is zero.BYoung's modulus is zero and bulk modulus is infinite.CYoung's modulus is infinite and bulk modulus is also infinite.DYoung's modulus is zero and bulk modulus is also zero.
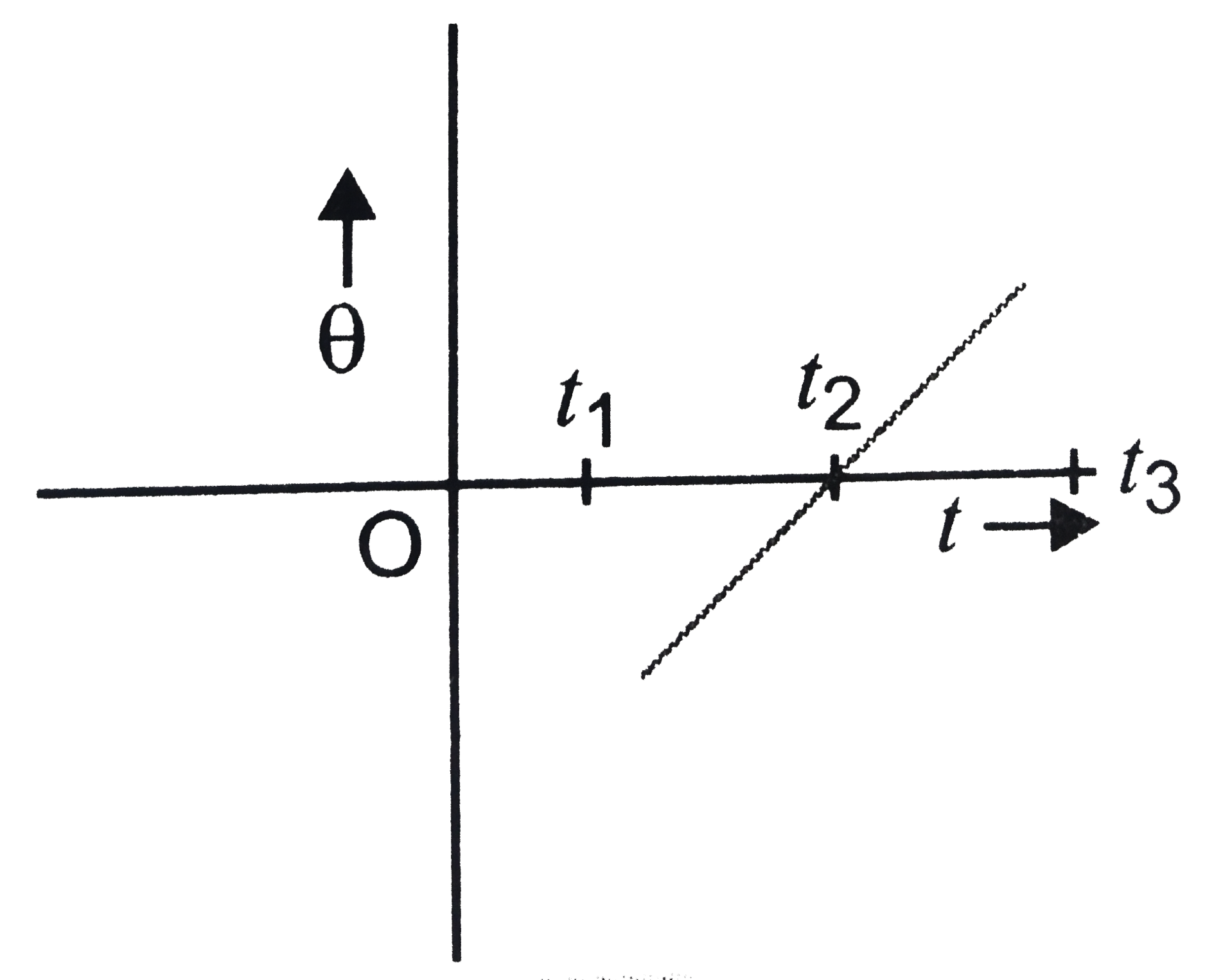
The variation of angular position θ, of a point on a rotating rigid body, with time t is shown in Fig. Is the body rotating clock wise or anti-clockwise ?
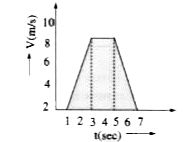
View SolutionFor the velocity - time graph shown in figure below the distance covered by the body in last two seconds of its motion is what fraction of the total distance covered by it in all the total distance covered by it in all the seven seconds
View SolutionElasticity of a rigid body is
View SolutionA body starts from rest and moves with constant acceleration. The ratio of distance covered by the body in nth second to that covered in n second is.
View SolutionDerive an equation for displacement of a projectile fired at an angle θ from the ground.
View SolutionDerive an expression for the rotational kinetic energy.
View SolutionWhat is the effect of force on a rigid body ?
View Solution