Can you calculate the torque acting on a rigid body without specifying a centre of rotation ?
To determine whether we can calculate the torque acting on a rigid body without specifying a center of rotation, we can follow these steps:
1. Understand the Definition of Torque:
Torque (τ) is defined as the product of the force (F) applied and the distance (r) from the point of rotation (or pivot) to the line of action of the force. Mathematically, it is expressed as:
τ=r×F
where r is the perpendicular distance from the axis of rotation to the line of action of the force.
2. Identify the Importance of the Center of Rotation:
The center of rotation is crucial because the torque depends on the distance from this point to where the force is applied. If we do not specify a center of rotation, we cannot determine the distance r.
3. Example of a Rigid Body:
Consider a wheel that is rolling. If a force is applied at a certain point on the wheel, the torque generated will depend on the distance from the center of the wheel (the center of rotation) to the point where the force is applied.
4. Conclusion:
Since torque is dependent on both the force applied and the distance from the center of rotation, it is impossible to calculate torque without specifying this center. Therefore, the answer to the question is no, we cannot calculate the torque acting on a rigid body without specifying a center of rotation.
Final Answer:
No, you cannot calculate the torque acting on a rigid body without specifying a center of rotation.
---
Torque (τ) is defined as the product of the force (F) applied and the distance (r) from the point of rotation (or pivot) to the line of action of the force. Mathematically, it is expressed as:
τ=r×F
where r is the perpendicular distance from the axis of rotation to the line of action of the force.
The center of rotation is crucial because the torque depends on the distance from this point to where the force is applied. If we do not specify a center of rotation, we cannot determine the distance r.
Consider a wheel that is rolling. If a force is applied at a certain point on the wheel, the torque generated will depend on the distance from the center of the wheel (the center of rotation) to the point where the force is applied.
Since torque is dependent on both the force applied and the distance from the center of rotation, it is impossible to calculate torque without specifying this center. Therefore, the answer to the question is no, we cannot calculate the torque acting on a rigid body without specifying a center of rotation.
No, you cannot calculate the torque acting on a rigid body without specifying a center of rotation.
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (VERY SHORT ANSWER QUESTIONS)
14 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM EQUATIONS OF ROTATIONAL MOTION)
8 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (LONG ANSWER QUESTIONS)
14 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
Knowledge Check
The torque acting on a body is the rotational, analogue of
Amass of the bodyBlinear kinetic energy of the bodyClinear velocity of the bodyDforce in linear motionAssertion: The motion of a ceiling fan is rotational only.
Reason: The motion of a rigid body which is pivoted fixed of rotation.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is false.DIf both assertion and reason are false.
What is the torque acting on a body moving with constant angular velocity ?
View SolutionWhat is the torque acting on a body moving with constant angular velocity ?
View SolutionShow that the torque acting on a body is equal to the product of moment of inertia and the angular acceleration of the body.
View SolutionIf the resultant torque of all the forces acting on a body is zero about a point is it necessary that it will be zero about any other point?
View SolutionS1: Net torque on a system due to all internal force about any point is zero.
S2: For rigid body undergoing fixed axis rotation, the direction of its angular acceleration and angular velocity
S3: if net torque on a rigid body about its centre of mass is zero, the angular speed of the rigid body is always zero.
S4: For a rigid body undergoing fixed axis rotation abouts its centre of mass, then net torque on rigid body about any point is same.
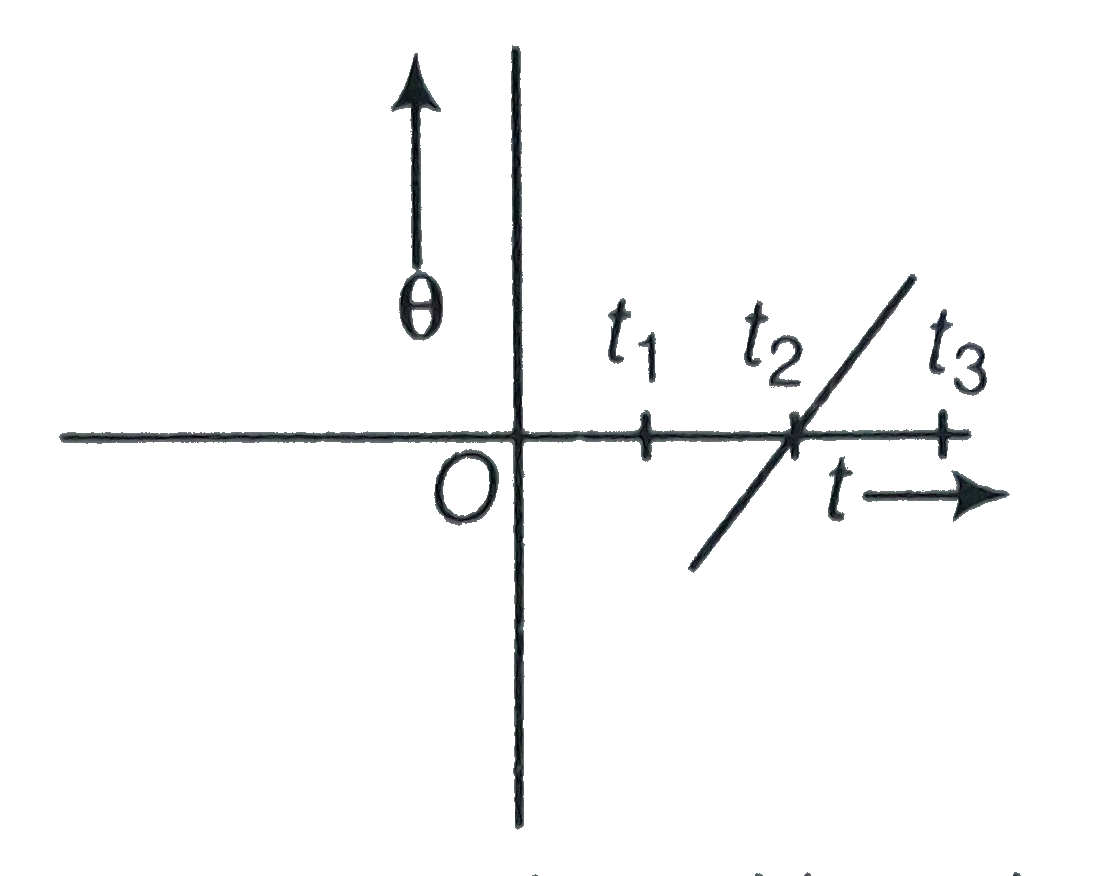
View Solutionthe variaton of angular postion θ of a point on a rotating rigid body with time t is shown in figure Is the body rotating clokwise or anti- clokwise ?
View Solution