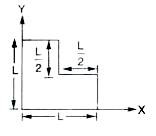
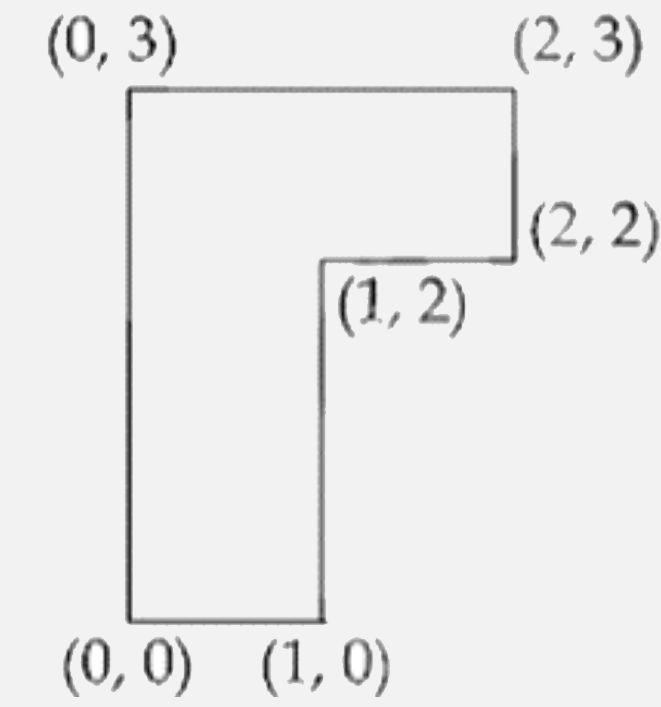
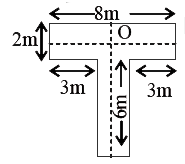Locate ,the centre of mass of the uniform then L-shaped body as shown in Fig. Assume its thickness to be t and density ρ.
L=r×mv=lcosθ×mgl
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ROTATIONAL KINETIC ENERGY , WORK ,POWER)24videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM MOMENT OF INERTIA, TORQUE)22videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS50videos
COMPETITION CARE UNIT
Similar Questions
Knowledge Check
- Question 1 - Select One
The x, y coordinates of the centre of mass of a uniform L-shaped lamina of mass 3 kg is
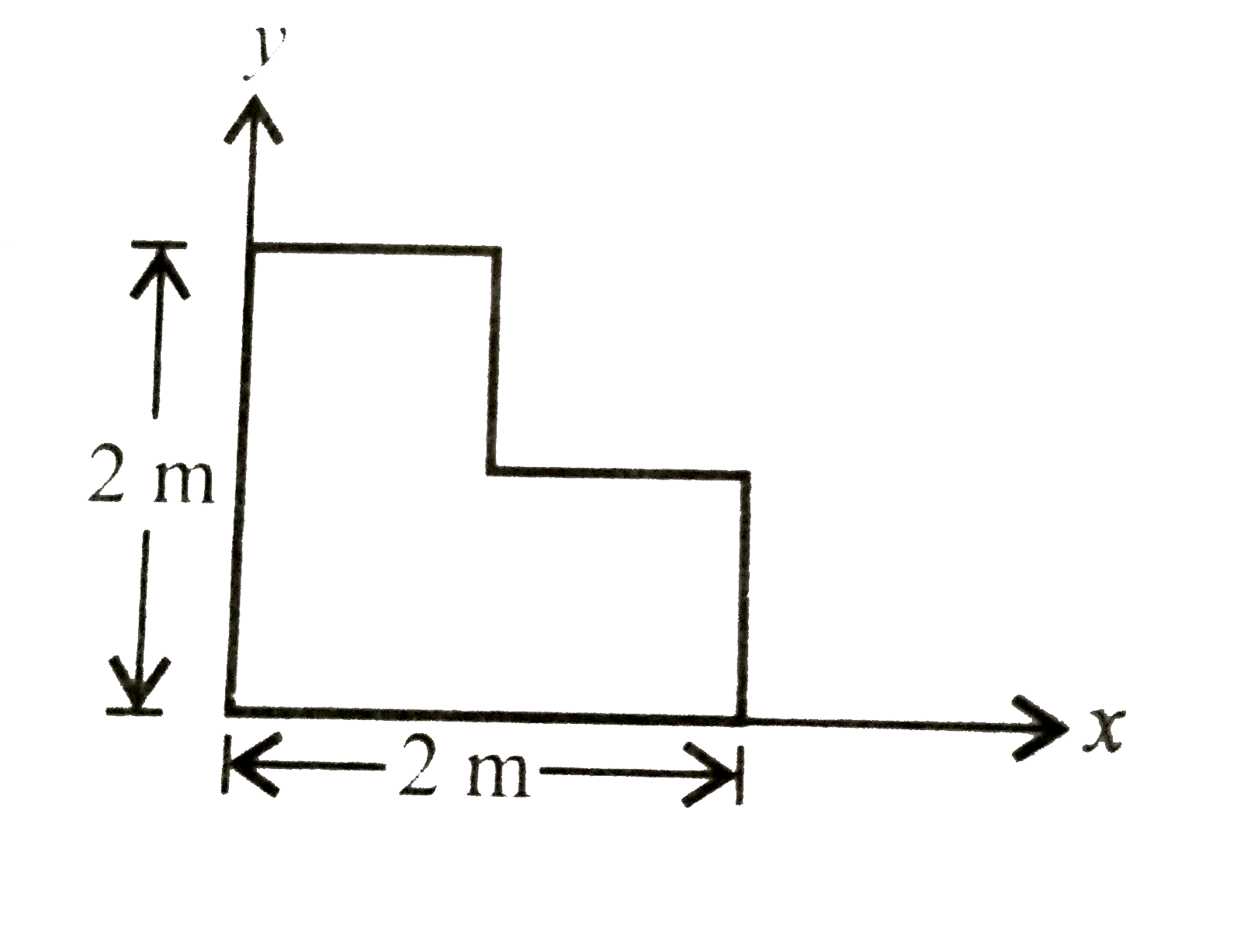A(5/6 m, 5/6 m)B(1 m, 1 m)C(6/5 m, 6/5 m)D(2 m, 2m) - Question 2 - Select One
The position of the centre of mass of a cube of uniform mass density will be at
Athe centre of one faceBthe centre of the interaction of diagonals of one face.Cthe geometric centre of the cubeDthe edge of a cube
What is the location of the centre of mass of a uniform triangular lamina ?
View SolutionFind the x coordinate of the centre of mass of the non - uniform rod of length L givne below. The origin is taken at the left end of the rod. The density of the rod as a function of its x- coordinates is ρ=ax2+bx+c, where a, b and c are constants.
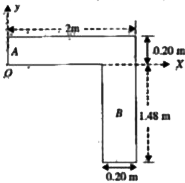
View SolutionFind the centre of mass of a uniform L shaped lamina (a thin flat plate) with dimension as shown in Fig. The mass of the lamina is 3kg.
View SolutionThe coordinates of the centre of mass of a uniform flag -shaped lamina (thin flat plate) of mass 4kg .( The coordinates of the same are shown in the figure) are :
View SolutionTwo identical uniform rods AB and CD, each of length L are jointed to form a T-shaped frame as shown in figure. Locate the centre of mass of the frame. The centre of mass of a uniform rod is at the middle point of the rod.
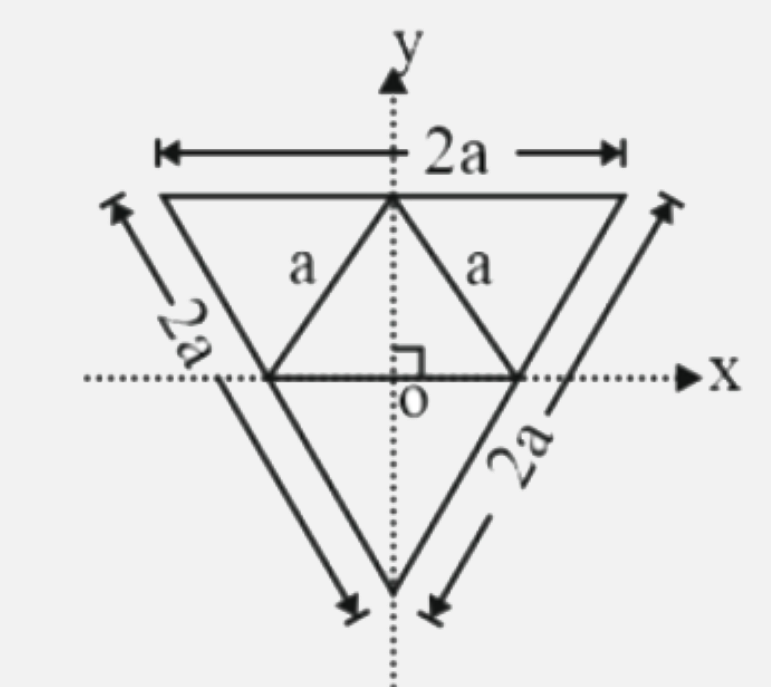
View SolutionThe y co - ordinate of the centre of mass of the system of three rods of length 2a and two rods of length a as shown in the figure is (Assume all rods to be of uniform density)
View Solution