A piece of wood of uniform cross section and height 15 cm floats vertically with its height 10 cm in water and 12 cm in spirit. Find the density of (i) wood and (ii) spirit
The correct Answer is:(i) 0.667gcm−3, (ii) 0.833gcm−3
To solve the problem, we will use Archimedes' principle, which states that the weight of the fluid displaced by a floating object is equal to the weight of the object itself. We will find the densities of both the wood and the spirit step by step.
Step 1: Understand the problem
We have a piece of wood with a total height of 15 cm. It floats in water with 10 cm submerged and in spirit with 12 cm submerged. We need to find the density of the wood and the density of the spirit.
Step 2: Calculate the density of wood using water
Using Archimedes' principle for the case of water:
- The volume of the wood (V_wood) = height × cross-sectional area = 15 cm × A
- The volume of the wood submerged in water (V_water) = 10 cm × A
- The density of water (ρ_water) = 1 g/cm³
According to Archimedes' principle:
Weight of water displaced=Weight of wood
This can be expressed as:
ρwater⋅Vwater⋅g=ρwood⋅Vwood⋅g
Since g (acceleration due to gravity) cancels out, we have:
ρwater⋅(10⋅A)=ρwood⋅(15⋅A)
Dividing both sides by A:
ρwater⋅10=ρwood⋅15
Substituting the value of ρ_water:
1⋅10=ρwood⋅15
ρwood=1015=23 g/cm3
ρwood=0.67 g/cm3
Step 3: Calculate the density of spirit using spirit
Now, we will find the density of the spirit using the same principle:
- The volume of the wood submerged in spirit (V_spirit) = 12 cm × A
- Let the density of spirit be ρ_spirit.
Using Archimedes' principle again:
ρwood⋅Vwood=ρspirit⋅Vspirit
Substituting the known values:
ρwood⋅(15⋅A)=ρspirit⋅(12⋅A)
Dividing both sides by A:
ρwood⋅15=ρspirit⋅12
Substituting the value of ρ_wood:
0.67⋅15=ρspirit⋅12
10.05=ρspirit⋅12
ρspirit=10.0512
ρspirit=0.8375 g/cm3
ρspirit≈0.83 g/cm3
Final Answers
(i) Density of wood = 0.67 g/cm³
(ii) Density of spirit = 0.83 g/cm³
We have a piece of wood with a total height of 15 cm. It floats in water with 10 cm submerged and in spirit with 12 cm submerged. We need to find the density of the wood and the density of the spirit.
Using Archimedes' principle for the case of water:
- The volume of the wood (V_wood) = height × cross-sectional area = 15 cm × A
- The volume of the wood submerged in water (V_water) = 10 cm × A
- The density of water (ρ_water) = 1 g/cm³
Weight of water displaced=Weight of wood
ρwater⋅Vwater⋅g=ρwood⋅Vwood⋅g
ρwater⋅(10⋅A)=ρwood⋅(15⋅A)
ρwater⋅10=ρwood⋅15
1⋅10=ρwood⋅15
ρwood=1015=23 g/cm3
ρwood=0.67 g/cm3
Now, we will find the density of the spirit using the same principle:
- The volume of the wood submerged in spirit (V_spirit) = 12 cm × A
- Let the density of spirit be ρ_spirit.
ρwood⋅Vwood=ρspirit⋅Vspirit
ρwood⋅(15⋅A)=ρspirit⋅(12⋅A)
ρwood⋅15=ρspirit⋅12
0.67⋅15=ρspirit⋅12
10.05=ρspirit⋅12
ρspirit=10.0512
ρspirit=0.8375 g/cm3
ρspirit≈0.83 g/cm3
(i) Density of wood = 0.67 g/cm³
(ii) Density of spirit = 0.83 g/cm³
Topper's Solved these Questions
- UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONBOOK - ICSECHAPTER - UPTHRUST IN FLUIDS, ARCHIMEDES' PRINCIPLE AND FLOATATIONEXERCISE - EXERCISE 5(c) (Multiple Choice Question)
3 Videos
- SOUNDBOOK - ICSECHAPTER - SOUNDEXERCISE - TOPIC 2 Infrasonic and Ultrasonic Waves ( 3 Marks Questions)
3 Videos
Similar Questions
Water rises to a height of 16.3 cm in a capillary of height 18 cm above the water leve. If the tube is cut at a height of 12 cm -
View SolutionA piece of wood floats in water with two-thirds of its volume submerged in water. In a certain oil it has 0.95 of its volume submerged. What is the density of wood and the oll?
View Solution
Knowledge Check
A U tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are at the same level with 10 cm of water in one arm and 12.5 cm of spirit in the other as shown in figure. The relative density of the spirit is
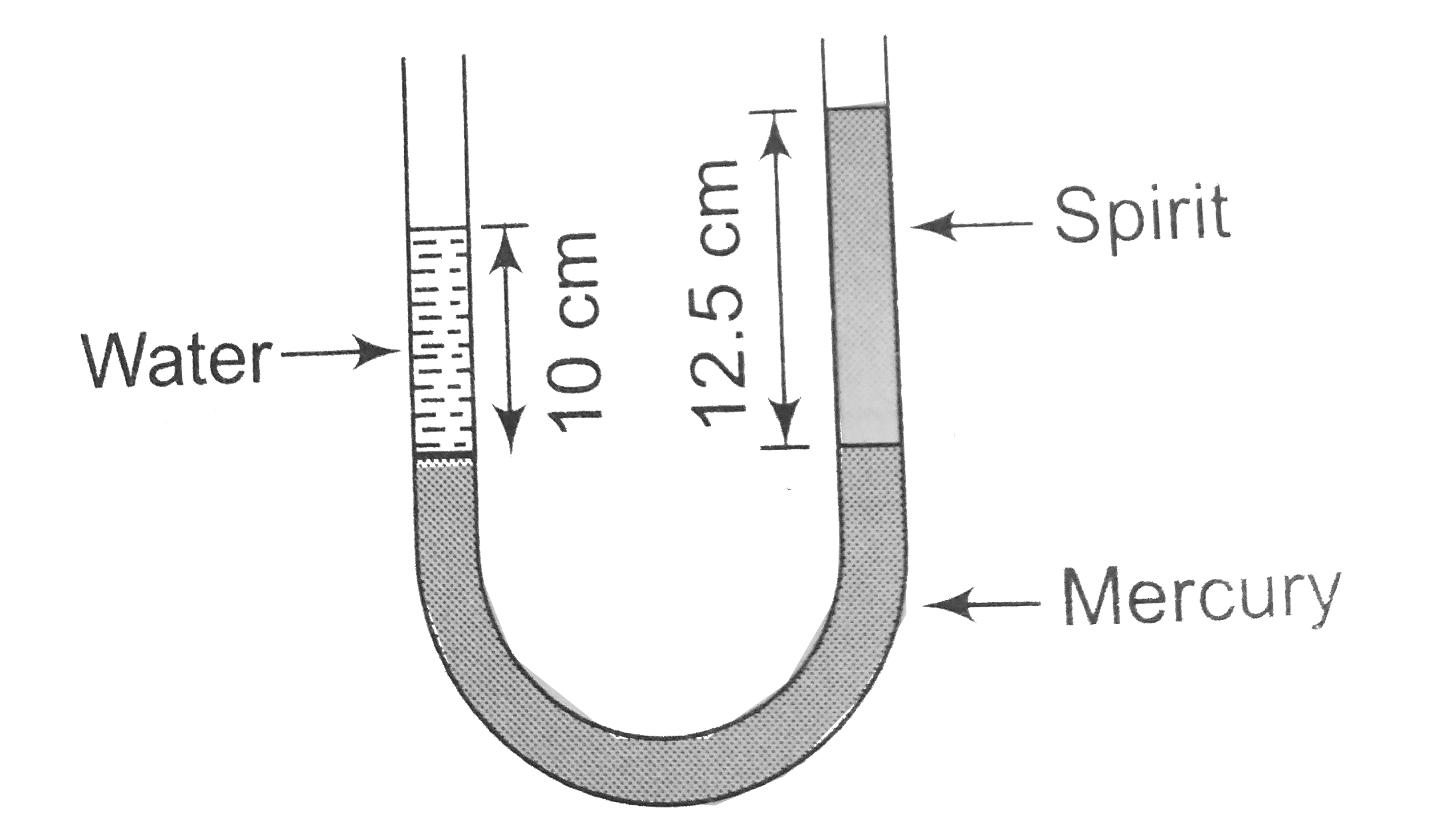 A0.6B0.8C1D1.25
A0.6B0.8C1D1.25
A body of uniform cross-sectional area floats in a liquid of density thrice its value. The portion of exposed height will be :
View SolutionThe radius of a cone is 5cm and vertical height is 12cm. Find the area of the curved surface.
View SolutionFind the area of a triangle with base 15 cm and height 8 cm.
View SolutionFind the area of a triangle :
whose height is 6 cm and base is 10 cm.
View SolutionA U tube contains water and methylated spirts separated by mercury columns in the two arms are in level with 10.0cm of water in one arm and 12.5 cm of spirit in the other. What is the relative density of spirit?
View SolutionA u tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are at the same levels with 10 cm of water in one arm and 12.5 cm of spirit on the other arm as shown. If 15 cm of water and spirit each are further poured into the respective arms of the tube. Difference in the level of mercury in the two arms is (Take, relative density of mercury = 13.6, relative density of spirit=0.8)
View SolutionA U tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are at the same level with 10 cm of water in one arm and 12.5 cm of spirit in the other as shown in figure. The relative density of the spirit is

View Solution
