A body of uniform cross-sectional area floats in a liquid of density thrice its value. The portion of exposed height will be :
2/3
5/6
1/6
1/3
The correct Answer is:A
To solve the problem of a body floating in a liquid where the density of the liquid is three times that of the body, we can follow these steps:
1. Define Variables:
- Let the density of the body be ρ.
- Therefore, the density of the liquid is 3ρ.
- Let the total height of the body be H.
- Let the height of the body that is exposed above the liquid surface be h.
- The submerged height of the body will then be H−h.
2. Apply the Principle of Buoyancy:
- According to Archimedes' principle, the weight of the body is equal to the buoyant force acting on it.
- The weight of the body can be expressed as:
W=mass×g=ρVg
where V is the volume of the body, which can be expressed as A×H (where A is the cross-sectional area).
3. Calculate the Volume of Displaced Liquid:
- The volume of the liquid displaced by the submerged part of the body is:
Vd=A×(H−h)
- The weight of the displaced liquid is:
Wd=density of liquid×volume of displaced liquid×g=(3ρ)×(A×(H−h))×g
4. Set Up the Equation:
- According to the equilibrium condition (weight of the body = weight of the displaced liquid):
ρ(A×H)g=(3ρ)(A×(H−h))g
- We can cancel g and A from both sides (assuming A≠0):
ρH=3ρ(H−h)
5. Simplify the Equation:
- Dividing both sides by ρ (assuming ρ≠0):
H=3(H−h)
- Expanding the right-hand side:
H=3H−3h
- Rearranging gives:
3h=3H−H
3h=2H
h=2H3
6. Conclusion:
- The portion of the exposed height h is 23 of the total height H.
- Therefore, the portion of the exposed height will be 23 of the total height.
Final Answer:
The portion of exposed height is 23 of the total height.
---
- Let the density of the body be ρ.
- Therefore, the density of the liquid is 3ρ.
- Let the total height of the body be H.
- Let the height of the body that is exposed above the liquid surface be h.
- The submerged height of the body will then be H−h.
- According to Archimedes' principle, the weight of the body is equal to the buoyant force acting on it.
- The weight of the body can be expressed as:
W=mass×g=ρVg
where V is the volume of the body, which can be expressed as A×H (where A is the cross-sectional area).
- The volume of the liquid displaced by the submerged part of the body is:
Vd=A×(H−h)
- The weight of the displaced liquid is:
Wd=density of liquid×volume of displaced liquid×g=(3ρ)×(A×(H−h))×g
- According to the equilibrium condition (weight of the body = weight of the displaced liquid):
ρ(A×H)g=(3ρ)(A×(H−h))g
- We can cancel g and A from both sides (assuming A≠0):
ρH=3ρ(H−h)
- Dividing both sides by ρ (assuming ρ≠0):
H=3(H−h)
- Expanding the right-hand side:
H=3H−3h
- Rearranging gives:
3h=3H−H
3h=2H
h=2H3
- The portion of the exposed height h is 23 of the total height H.
- Therefore, the portion of the exposed height will be 23 of the total height.
The portion of exposed height is 23 of the total height.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Surface Tension)
26 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Thermal Physics) (Temperature scales & thermal expansion)
13 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Fluid Dynamics + Viscosity)
18 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
View Solution
Knowledge Check
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
AT∝1√mBT∝√ρCT∝1√ADT∝1ρ
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is givan a small vertical displacement from equilibrium, it undergoes oscillation with a time period T, then select the wrong alternative.
View SolutionThe vessel shown in the figure has two sections of areas of cross-section A1andA2. A liquid of density ρ fills both the section, up to a height h in each. Neglect atmospheric pressure. Choose correct options.
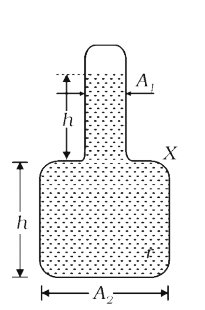
View SolutionConsider a solid cylinder of the density ρs cross section area A and h ploating in a liquid of density ρl as shown in figure (ρl>ρs) . It is depressed sligtly and allowed to oscillation.

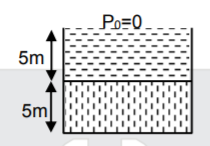
View SolutionTwo liquid columns of same height 5m and densities ρ and 2ρ are filled in a container of uniform cross sectional area. Then ratio of force exerted by the liquid on upper half of the wall to lower half of the wall is.
View SolutionA block of rectangular size of mass m and area of cross section A, float in a liquid of density ρ.If we give a small vertical displacement from equilibrium, It undergoes SHM with time period T, then
View SolutionA solid cylinder of denisty ρ0, cross-section area A and length l floats in a liquid ρ(>ρ0 with its axis vertical, . If it is slightly displaced downward and released, the time period will be :
View SolutionA horizontal tube of uniform cross-sectional area A is bent in the form of U as shown in figure. If the liquid of density ρ enters and leaves the tube with velcity v, then the extermal force F requried to hold the bend stationary is

View Solution
