Two forces each of magnitude 2N act vertically upwards and downwards respectively at the two ends of a uniform rod of length 1m which is pivoted at its centre. Draw a diagram of the arrangement and determine the resultant moment of forces about the mid point of the rod.
To solve the problem step by step, we will follow these instructions:
Step 1: Draw the Diagram
First, we need to visualize the problem. Draw a horizontal rod of length 1 meter, pivoted at its center. Mark the two ends of the rod as points A and B.
- Point A: This is the left end of the rod where a force of 2N acts vertically upwards.
- Point B: This is the right end of the rod where a force of 2N acts vertically downwards.
Step 2: Identify the Forces
In our scenario:
- At point A (left end), a force of 2N acts upwards.
- At point B (right end), a force of 2N acts downwards.
Step 3: Calculate the Perpendicular Distance
Since the rod is pivoted at the center, the distance from the pivot (midpoint) to each end (A and B) is:
- Distance from pivot to A = 0.5 meters
- Distance from pivot to B = 0.5 meters
Step 4: Calculate the Moment of Forces
The moment of a force about a pivot point is calculated using the formula:
Moment=Force×Perpendicular Distance
Moment at Point A (Clockwise):
- Force = 2N
- Perpendicular Distance = 0.5m
Moment at A=2N×0.5m=1N m
Moment at Point B (Counterclockwise):
- Force = 2N
- Perpendicular Distance = 0.5m
Moment at B=2N×0.5m=1N m
Step 5: Determine the Resultant Moment
Since both moments are acting in the same direction (clockwise), we can add them together to find the resultant moment:
Resultant Moment=Moment at A+Moment at B
Resultant Moment=1N m+1N m=2N m
Final Answer
The resultant moment of forces about the midpoint of the rod is 2 N m in the clockwise direction.
---
First, we need to visualize the problem. Draw a horizontal rod of length 1 meter, pivoted at its center. Mark the two ends of the rod as points A and B.
- Point B: This is the right end of the rod where a force of 2N acts vertically downwards.
In our scenario:
- At point A (left end), a force of 2N acts upwards.
- At point B (right end), a force of 2N acts downwards.
Since the rod is pivoted at the center, the distance from the pivot (midpoint) to each end (A and B) is:
- Distance from pivot to A = 0.5 meters
- Distance from pivot to B = 0.5 meters
The moment of a force about a pivot point is calculated using the formula:
Moment=Force×Perpendicular Distance
- Force = 2N
- Perpendicular Distance = 0.5m
Moment at A=2N×0.5m=1N m
- Force = 2N
- Perpendicular Distance = 0.5m
Moment at B=2N×0.5m=1N m
Since both moments are acting in the same direction (clockwise), we can add them together to find the resultant moment:
Resultant Moment=Moment at A+Moment at B
Resultant Moment=1N m+1N m=2N m
The resultant moment of forces about the midpoint of the rod is 2 N m in the clockwise direction.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1A27videos
FORCE
- BOOK - ICSECHAPTER - FORCE EXERCISE - EXERCISE 1(A) Multiple choice questions2videos
FORCE
- BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS1videos
ELECTRO-MAGNETISM
- BOOK - ICSECHAPTER - HOUSEHOLD CIRCUITS EXERCISE - EXERCISE -9(B) (MULTIPLE CHOICE TYPE)2videos
HOUSEHOLD CIRCUITS
Similar Questions
The forces each of magnitude 10N act vertically upwards and downwards respectively at the two ends A and B of a uniform rod of length 4m which is pivoted at its mid point O as shown is fig. 1.30, Determine the magnitude of the resultant moment of forces about the pivot O.
 View Solution
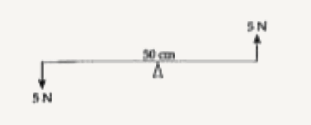
View SolutionTwo forces each of 5 N act vertically upwards and downwards respectively on the two ends of a uniform meter rule which is placed at its mid-point as shown in the diagram. Determine the magnitude of the resultant moment of these forces about the midpoint.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two forces each of magnitude 2N, act at an angle of 60∘. The magnitude of the resultant force
A√1.1 NewtonB√4 NewtonC√12 NewtonD√14.9 Newton
Two forces each of magnitude 5 N are applied in opposite directions at the ends of a uniform nod of length 0.5 m. Draw diagram of the arrangement and find the total moment of the two forces.
View SolutionThe moment of inertia of a uniform rod of mass 0.50 kg and length 1 m is 0.10 kg m^2 about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.
 View Solution
View SolutionA uniform rod of length 60 cm and mass 6kg is acted upon by two forces as shown in the diagram. The force exerted by 45 cm part ofthe rod on 15 cm part of the rod is
 View Solution
View SolutionTwo forces of magnitude 8 N and 15 N respectively act at a point . If the resultant force is 17 N , the angle between the forces has to be
View Solution

