A coolie X carrying a load on his head climbs up a slope and another coolie Y carrying the identical load on his head moves the same distance on a frictionless horizontal platform. Who does more work. Explain the reason
To determine who does more work between coolie X climbing a slope and coolie Y moving on a horizontal platform, we can analyze the work done by each coolie step by step.
Step 1: Understand the Concept of Work
Work is defined as the product of force and displacement in the direction of the force. Mathematically, it can be expressed as:
Work=Force×Displacement×cos(θ)
where θ is the angle between the force and the direction of displacement.
Step 2: Analyze Coolie X's Work
Coolie X is climbing a slope while carrying a load. The force he exerts is equal to the weight of the load, which can be expressed as:
Force=m⋅g
where m is the mass of the load and g is the acceleration due to gravity.
As he climbs the slope, he is also gaining height. If the height of the slope is h, the work done by coolie X can be calculated as:
WorkX=m⋅g⋅h
This is because he is working against gravity to lift the load to height h.
Step 3: Analyze Coolie Y's Work
Coolie Y is moving on a frictionless horizontal platform. In this case, the height remains constant (zero), and he is not working against gravity to lift the load. The work done by coolie Y can be expressed as:
WorkY=0
since there is no vertical displacement.
Step 4: Compare the Work Done
Now we can compare the work done by both coolies:
- Work done by coolie X: WorkX=mgh
- Work done by coolie Y: WorkY=0
From this comparison, it is clear that:
WorkX>WorkY
Conclusion
Coolie X does more work than coolie Y because he is lifting the load to a height h against the force of gravity, while coolie Y is not doing any work against gravity as he moves horizontally.
Work is defined as the product of force and displacement in the direction of the force. Mathematically, it can be expressed as:
Work=Force×Displacement×cos(θ)
where θ is the angle between the force and the direction of displacement.
Coolie X is climbing a slope while carrying a load. The force he exerts is equal to the weight of the load, which can be expressed as:
Force=m⋅g
where m is the mass of the load and g is the acceleration due to gravity.
WorkX=m⋅g⋅h
This is because he is working against gravity to lift the load to height h.
Coolie Y is moving on a frictionless horizontal platform. In this case, the height remains constant (zero), and he is not working against gravity to lift the load. The work done by coolie Y can be expressed as:
WorkY=0
since there is no vertical displacement.
Now we can compare the work done by both coolies:
- Work done by coolie X: WorkX=mgh
- Work done by coolie Y: WorkY=0
WorkX>WorkY
Coolie X does more work than coolie Y because he is lifting the load to a height h against the force of gravity, while coolie Y is not doing any work against gravity as he moves horizontally.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - WORK ENERGY AND POWEREXERCISE - EXERCISE-2(A) (MULTIPLE CHOICE TYPE )2videos
WORK ENERGY AND POWER
- BOOK - ICSECHAPTER - WORK ENERGY AND POWEREXERCISE - EXERCISE-2(A) (NUMERICALS)16videos
WORK ENERGY AND POWER
- BOOK - ICSECHAPTER - WORK ENERGY AND POWEREXERCISE - EXERCISE-2(C ) NUMERICALS6videos
WORK ENERGY AND POWER
- BOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)15videos
CALORIMETRY
Similar Questions
A coolie carrying a load on his head and moving on a frictionless horizontal platform does no work. Explain the reason why.
View SolutionA man having a box on his head, climbs up a slope and another man having an identical box walks the same distance on a levelled road. Who does more work against the force of gravity and why?
View Solution
Knowledge Check
- Question 1 - Select One
A weight lifter lifts a load of 250N while a coolie lifts same load on his head. If the height of weight lifter and coolie is same, compare the work done?

 AWork done is sameBwork done by coolie is moreCwork done by weight lifter is moreDnone of the above
AWork done is sameBwork done by coolie is moreCwork done by weight lifter is moreDnone of the above - Question 2 - Select One
A man weighing 60 kg climbs up a staircase carrying a load of 20 kg on his head. The stair case has 20 steps each of height 0.2 m. If he takes 10 s to climb find his power
A313.6 WB120.6 WC510 WD0
A man carries a load on his head through a distance of 5 m. The maximum amount of work is done when he
View SolutionA man carries a load of 5 kg on his head through a distance of 10 m. the minimum amount of work is done when he
View SolutionA coolie 1.5 m tall raises a load of 80 kg in 2 sec from the ground to his head and then walks a distance of 40 m in another 2 second. The power developed by the coolie is : (g=10m/s2)
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
The ratio of the energy consumed by the camel during uniform motion for the two cases when it moves with speed 5ms−1 to the case when it moves with 10ms−1View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
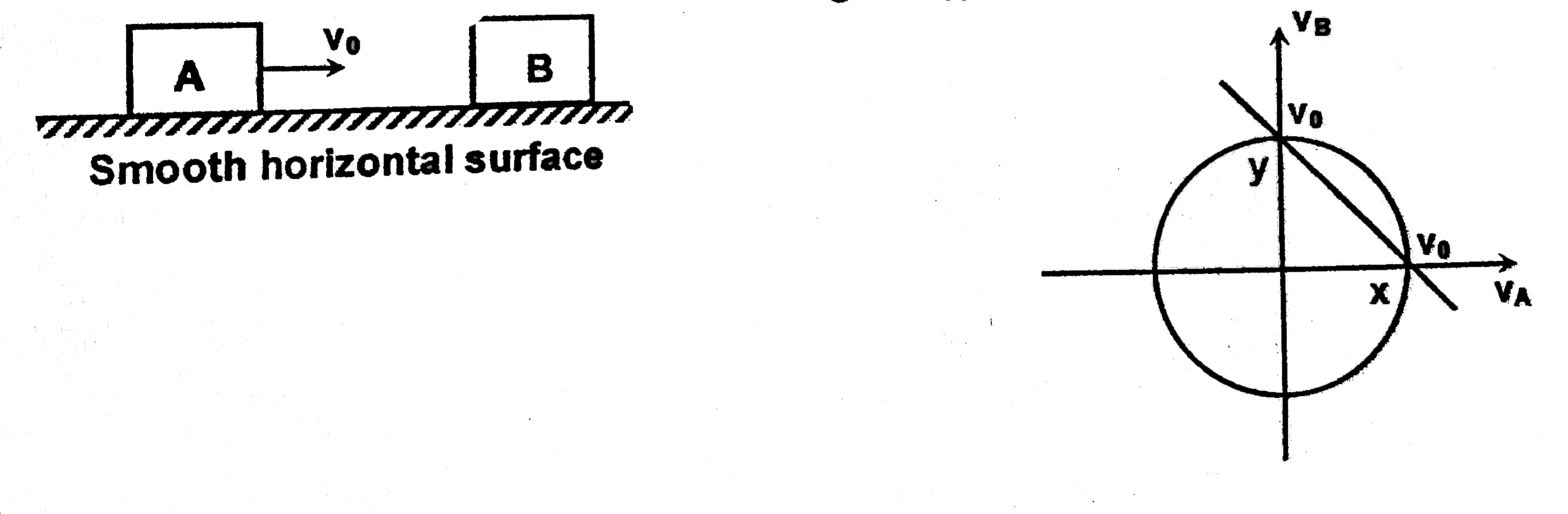
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
In a situation block A is moving with velocity 2m/s an strikes another identical block B kept at rest. The vA−vB plot for the situation is shown. m and l are the intersection points whose vA,vB coordinaes are given in the figure. The coefficient of restitution of the collision is
 View Solution
View SolutionGraphical soluton of a two body head on collision
A block A of mass m moving with a uniform velocity v0 strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.
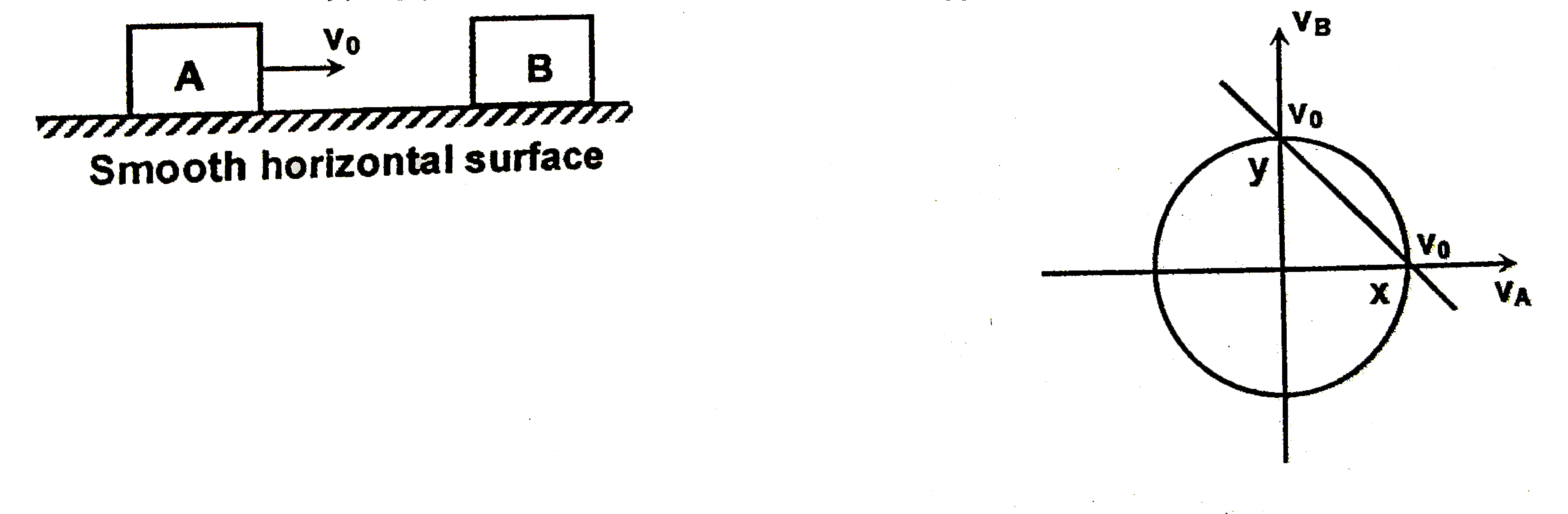
So mv0=mvAmvB (vA and vB are the velocities of the blocks after collision)
∴v0=vA+vB.........(i)
If the collision is perfectly elastic
12mv20=12mv2A+12mv2B
⇒v20=v2A+v2B......(ii)
Both the above equation (i) and (ii) are plotted on vA−vB plane as shown in figure (ii). This plot can be used to find the unknowns vA and vB.
For example the solution of the situation in figure (i) is vA=0,vB=v0 (point y in the plot)
Because vA=v0,vB=0 (point x in the plot) is not physically possible.
If the collision is perfectly inelastic, then the vA−vB plot isView Solution

