The path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
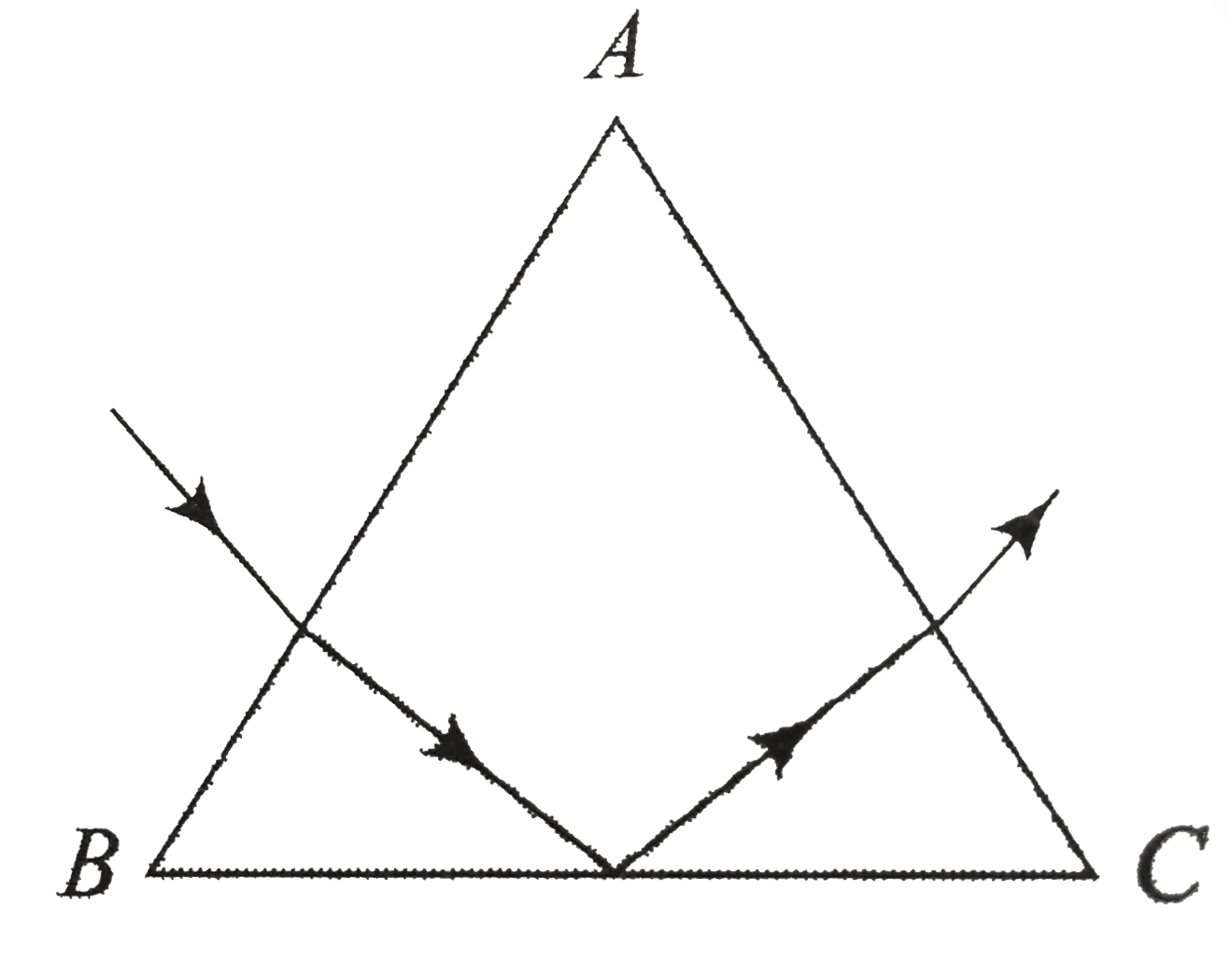
In the figure shown,
r2=C
r1=60−r2=60−C
r3=60−r2=60−C
r1=r3=r (say)
i1=i2=i (say)
Net deviation, δ=(1−r)+(180−2r2)+(i−r)=108∘
r2=r−i=36∘
C+60−C−i=36∘
i=24∘,sin24∘≈0.40
Form Snell's law, we have
sin24∘=μsinr
0.4=μsin(60∘−C)
0.4=μ[√32cosC−12μ]
0.8=√3μ√1−1μ2−1
∴μ2−1=1.08
μ=1.447
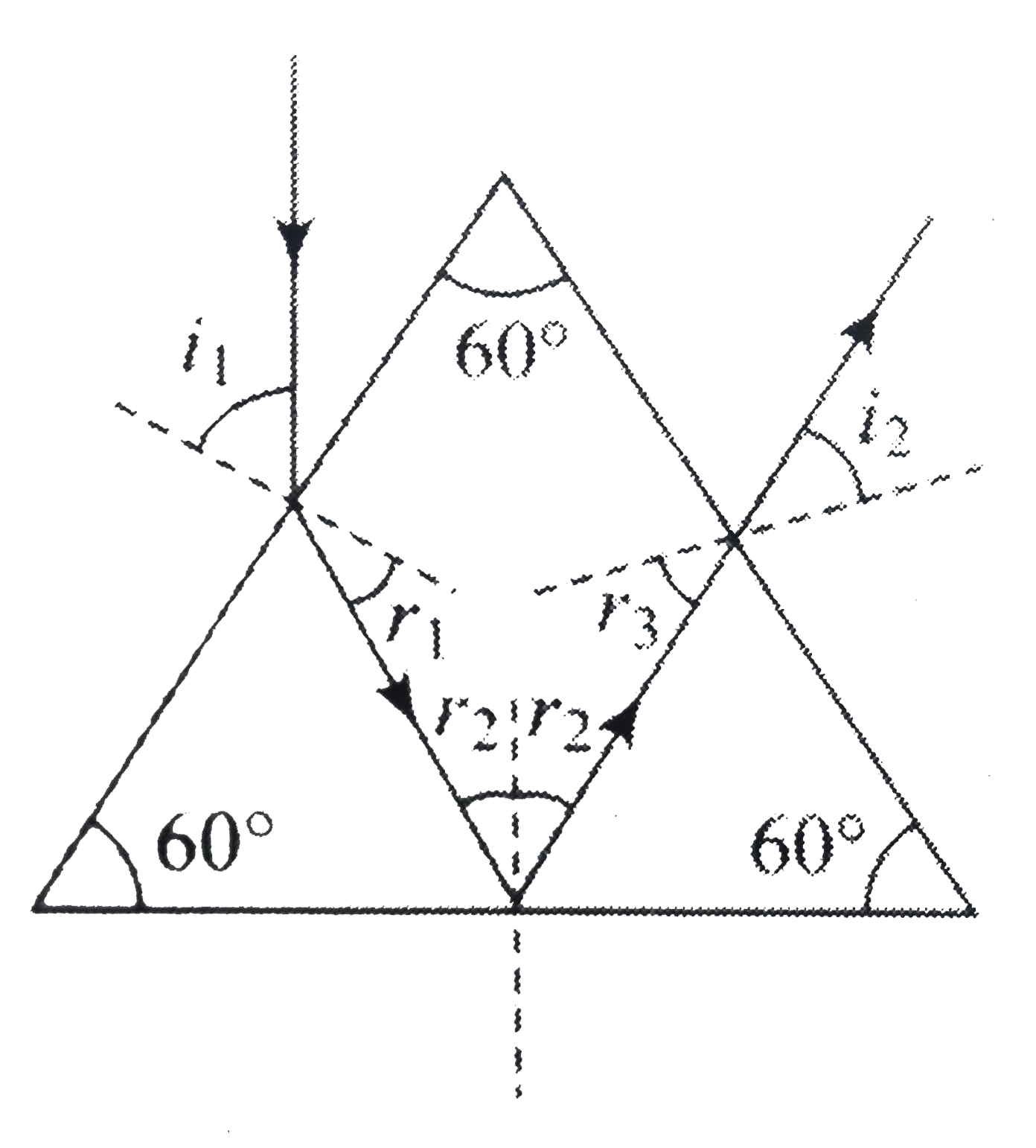
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.5
22 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.6
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.3
25 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A ray of light-is incident on glass at the polarising angle ip. Find the angle between the reflected and refracted rays.
View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60∘ so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
View Solution
Knowledge Check
A ray of light is incident normally on the prism (μ=32) immersed in a liquid as shown in the figure. The largest value for the angle α so that ray is totally reflected at the face AC is 30∘. The refractive index of the given liquid is
 A√32B34C43D3√34
A√32B34C43D3√34A total reflecting equilateral prism can be used to deviate a ray of light through :
A30∘B60∘C75∘D90∘
The figure shows the path of a ray passing through an equiangular prism PQR. It is incident on face PR at angle slightly greater than the critical angle for total internal reflection . If the angle α shown in the figure is 30∘ . Calculate the R.I. of the material of the prism.
_E01_145_Q01.png)
View SolutionA ray of light is incident normally on one of the faces of a prism of apex angle 30 degree and refractive index √2. The angle of deviation of the ray in degrees is
View SolutionUnder what conditions is the phenomenon of total internal reflection between the critical angle of incidence and the refractive index of the medium.
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
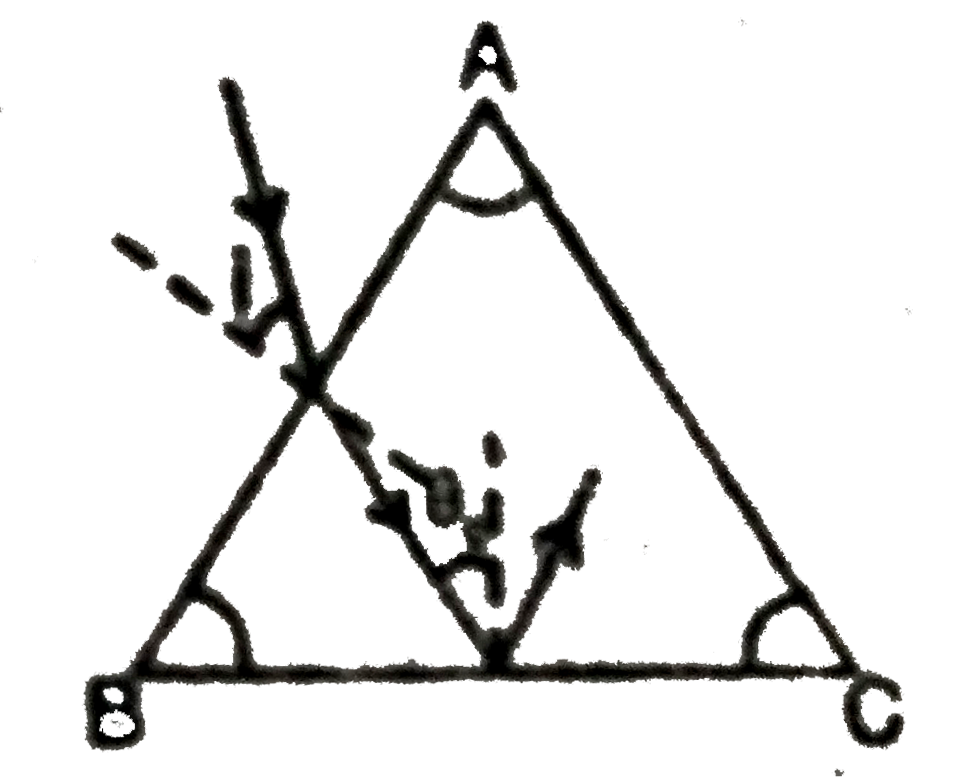
View SolutionA light is incident on face AB of an equilateral glass prism ABC. After refraction at AB, the ray is incident on face BC at the angle slightly greater than critical angle so that it gets reflected from face BC and finally emerges out from face AC. Net deviation angle of the ray is 112∘ anticlockwise. The angle of incidence 'i' has value:
View SolutionA light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r,r1,e and the total deviation after two refractions.

View Solution