ਚਿੱਤਰ 6.44 ਵਿੱਚ ਇਕੋ ਆਧਾਰ BC ਉੱਤੇ ਦੋ ਤ੍ਰਿਭੁਜ ABC ਅਤੇ DBC ਬਣੇ ਹੋਏ ਹਨ। ਜੇਕਰ AD,BC ਨੂੰ O 'ਤੇ ਕੱਟੇ ਤਾਂ ਦਰਸਾਉ ਕਿ ar(ABC)ar(DBC)=AODO ਹੈ।
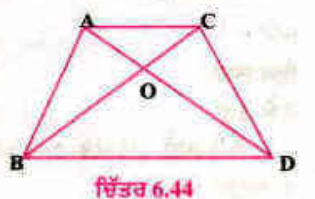
Step by step video & image solution for ਚਿੱਤਰ 6.44 ਵਿੱਚ ਇਕੋ ਆਧਾਰ BC ਉੱਤੇ ਦੋ ਤ੍ਰਿਭੁਜ ABC ਅਤੇ DBC ਬਣੇ ਹੋਏ ਹਨ। ਜੇਕਰ AD,BC ਨੂੰ O 'ਤੇ ਕੱਟੇ ਤਾਂ ਦਰਸਾਉ ਕਿ (ar (ABC))/(ar (DBC))=(AO)/(DO) ਹੈ। by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ਚਿੱਤਰ 6.16 ਵਿੱਚ PSsQ=PTTR ਹੈ ਅਤੇ ∠PST=∠PRQ ਹੈ। ਸਿੱਧ ਕਰੋ ਕਿ ΔPQR ਇੱਕ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ।
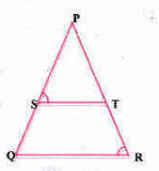
View Solutionਜੇਕਰ tanA=43, ਤਾਂ ਕੋਣ A ਦੇ ਬਾਕੀ ਤਿਕੋਣਮਿਤਈ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ।
View Solutionਜਾਂਚ ਕਰੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਮੀਕਰਣਾਂ ਦੋ ਘਾਤੀ ਹਨ ਜਾਂ ਨਹੀ : (x+1)2=2(x−3)
View SolutionIn Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that (ar (ABC))/( ar (DBC))= (AO )/( DO )
View SolutionIn the given figure,Delta ABC and Delta DBC are on the same base BC.If AD intersects BC at O , prove that (ar(Delta ABC))/(ar(Delta DBC))=(AO)/(DO)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the given figure, AB is a diameter, O is the center of the circle and ∠OCB=50∘ then find ∠DBC.
View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solutionआकृति 6 .44 में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए है यदि AD , BC को O पर प्रतिच्छेद करे , तो दर्शाइए कि ar(ABC)ar(DBC)=AODO है

View SolutionIn the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
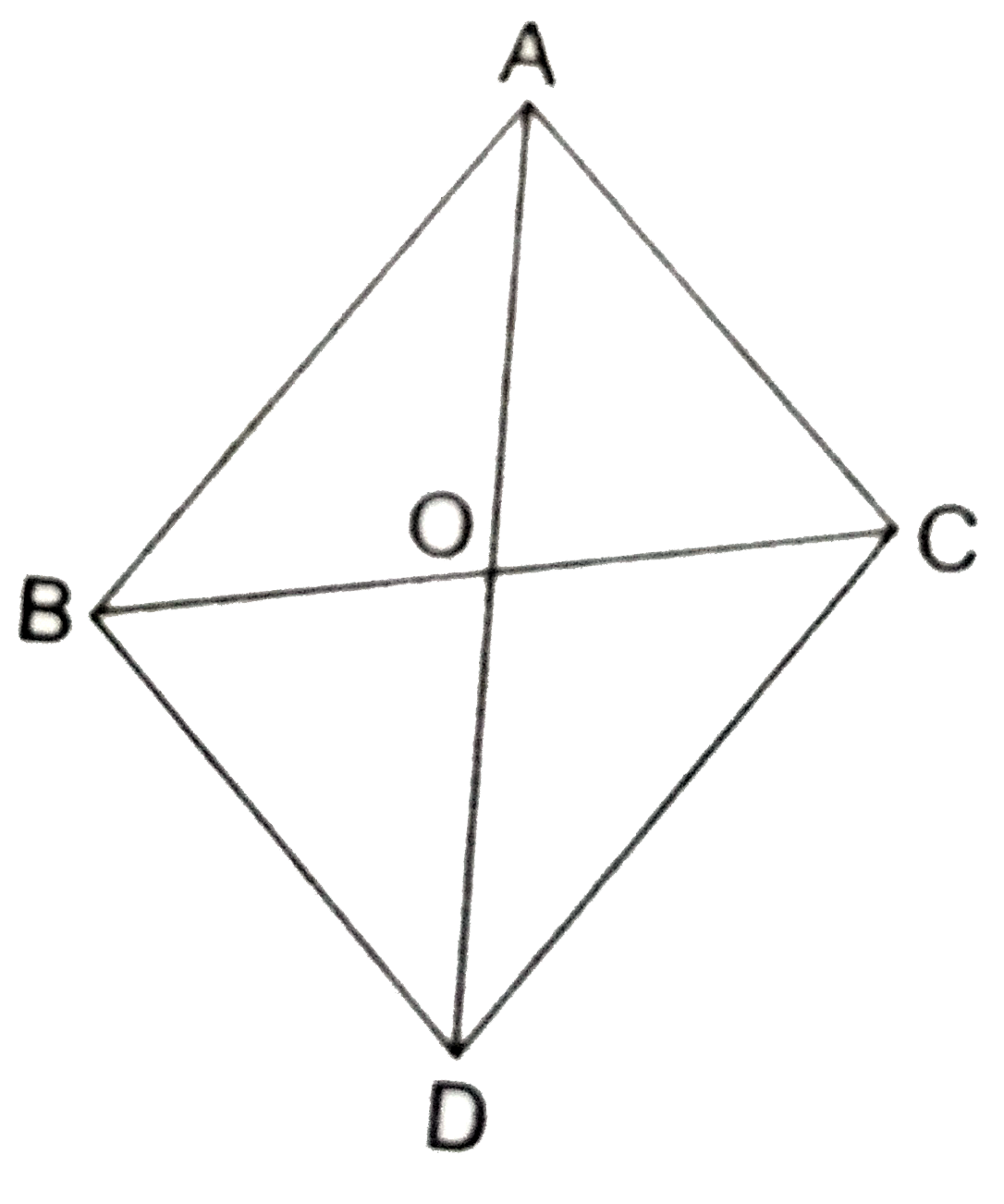
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
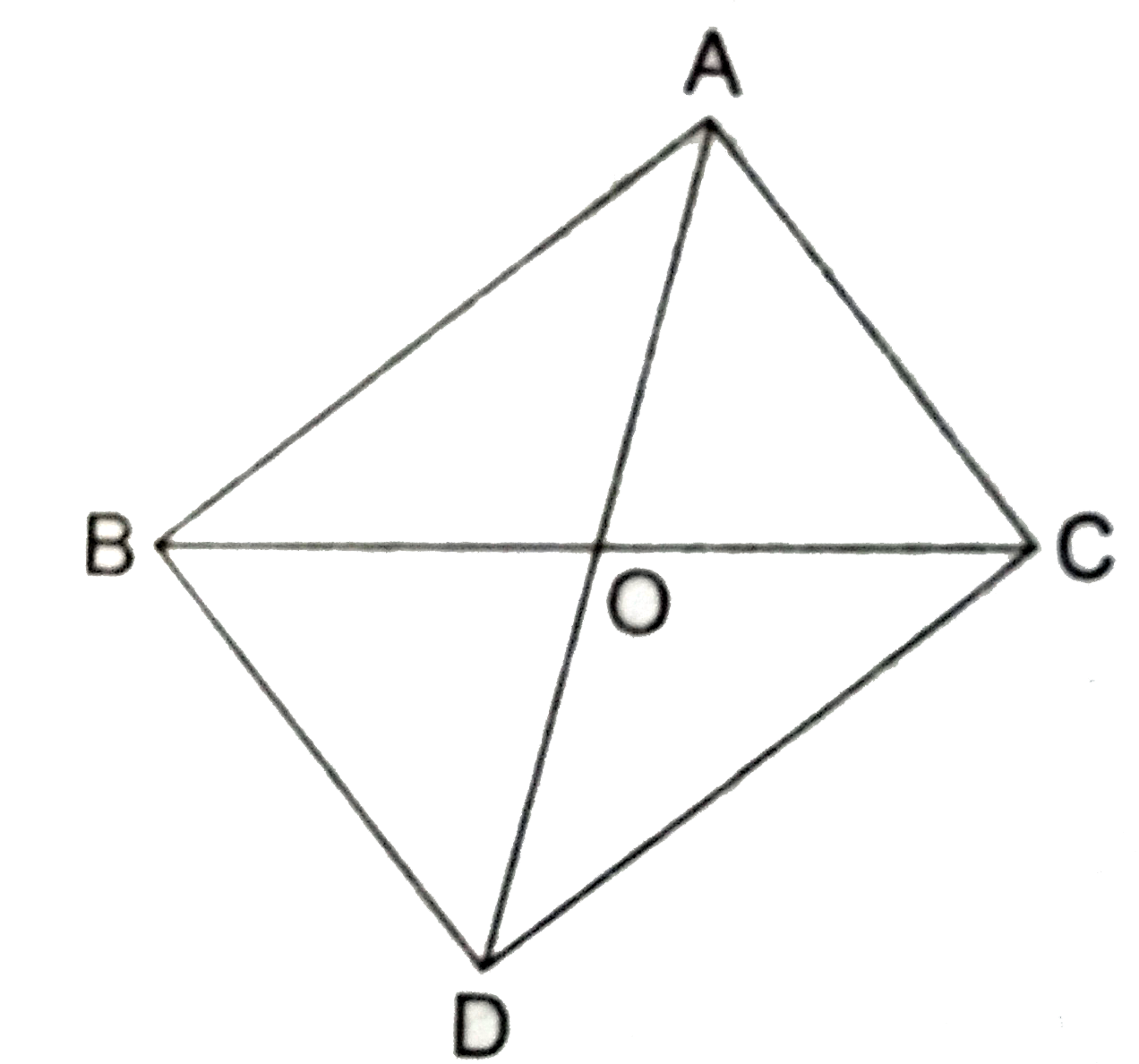
View Solutionआकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए है। यदि AD,BD को O पर प्रतिच्छेद पर तो दर्शाइए कि ar(ΔABC)ar(ΔDBC)=AODO है।
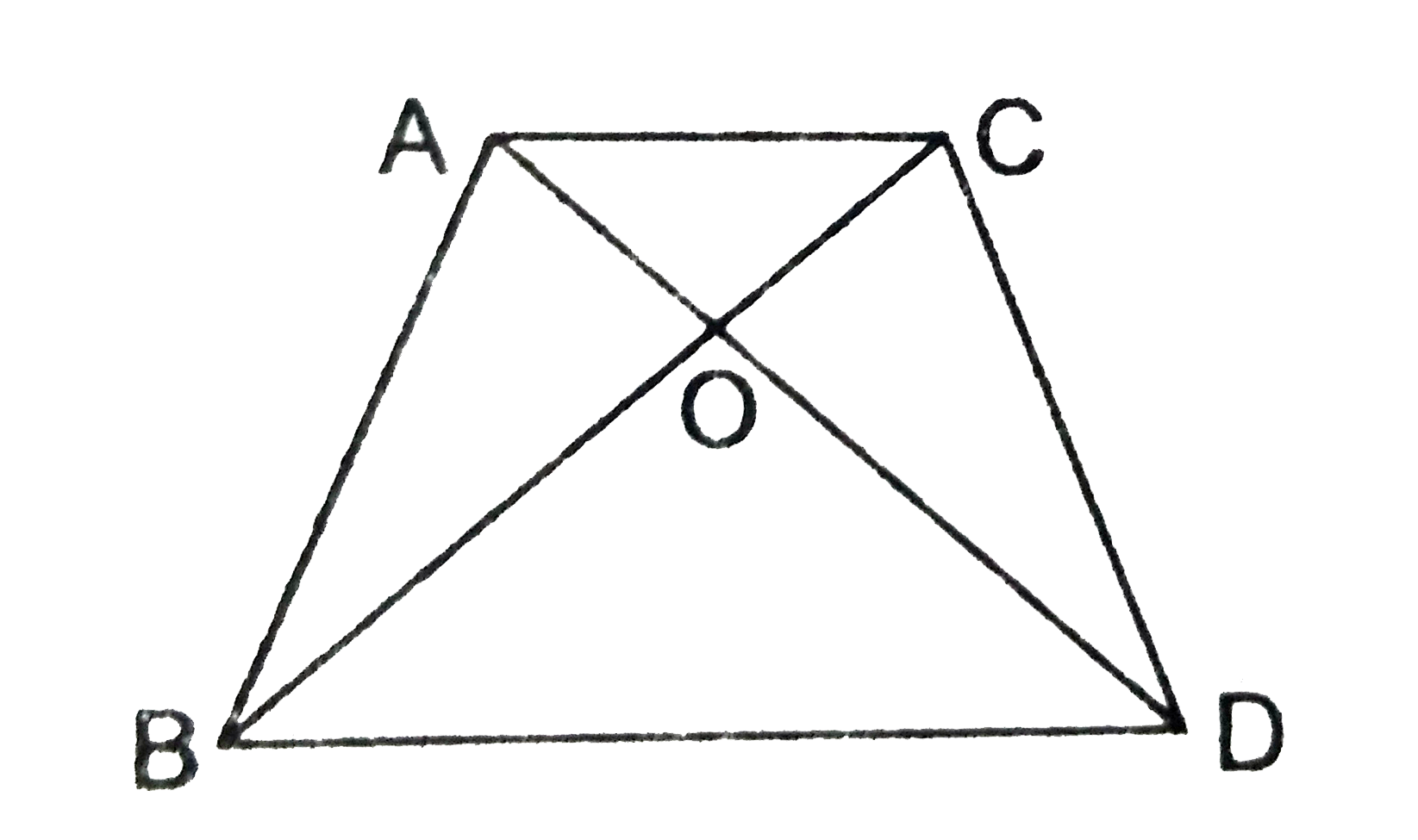
View SolutionIn Fig , ABC and DBC are two triangles on the same base BC. If AD intersects BC,at O , show that ar(ABC)ar(DBC)=AODO
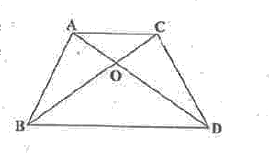
View SolutionΔABC and ΔBDC are on the same base BC. Prove that ar(ΔABC)ar(ΔDBC)=AODO
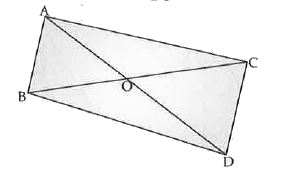
View Solution
