The disintegration rate for a sample containing 6027Co as the only radioactive nuclide, is found to be 240 atoms/minute. t12 of Co is 5.2 years. Find the number of atoms of Co in the sample. How long must this radioactive sample be maintained before the rate falls to 100 disintegrations/minutes
9.6×108, 6.6 years
Topper's Solved these Questions
- ATOMIC STRUCTURE AND RADIOACTIVITYBOOK - RC MUKHERJEECHAPTER - ATOMIC STRUCTURE AND RADIOACTIVITYEXERCISE - Objective Problems
66 Videos
- ATOMIC STRUCTURE AND RADIOACTIVITYBOOK - RC MUKHERJEECHAPTER - ATOMIC STRUCTURE AND RADIOACTIVITYEXERCISE - Objective Problems
66 Videos
- ATOMIC WEIGHTBOOK - RC MUKHERJEECHAPTER - ATOMIC WEIGHTEXERCISE - PROBLEMS
6 Videos
Similar Questions
A radioactive sample has N0 active at t=0 . If the rate of disintegration at any time is R and the number of atoms is N, them the ratio R/N varies with time as.
View SolutionA radioactive sample had an initial activity of 56 dpm . After 69.3 minutes, it was found to have an activity of 28 dpm . Find the number of atoms in a sample having an activity of 100 dpm.
View Solution
Knowledge Check
A radioactive sample has N0 active at t=0 . If the rate of disintegration at any time is R and the number of atoms is N, them the ratio R/N varies with time as.
A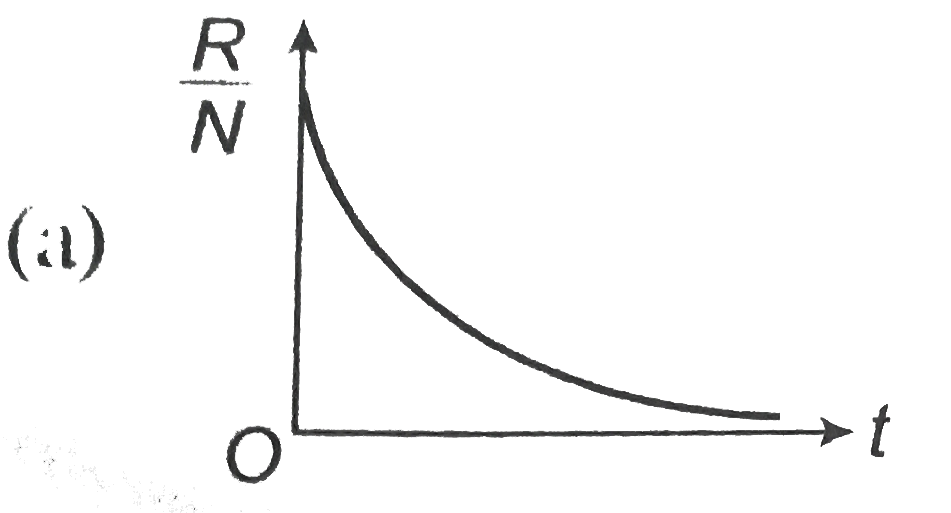 .B
.B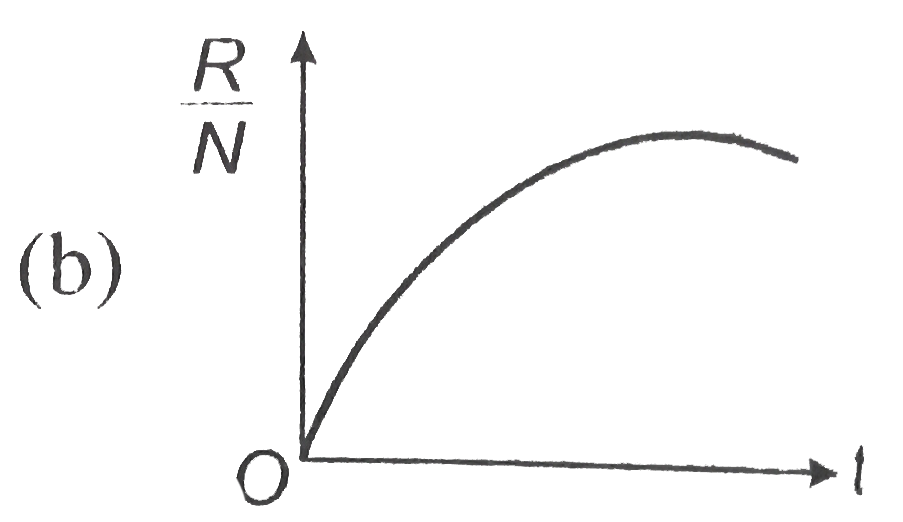 .C
.C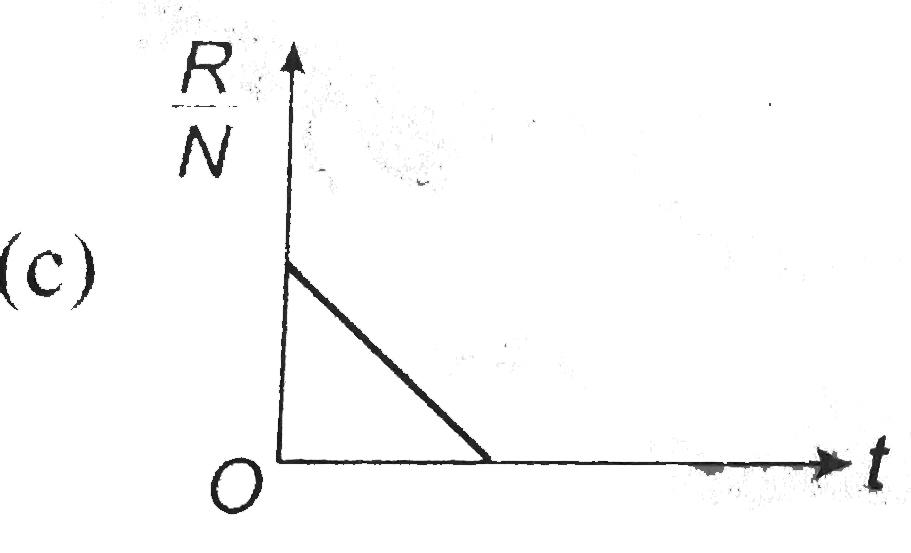 .D
.D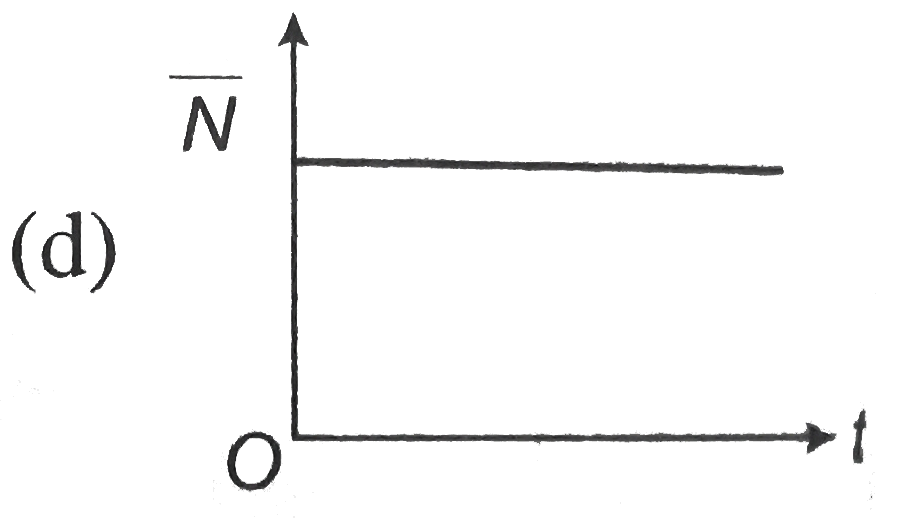 .
.Find the decay constant (per minute) of a radioactive sample if at any instant its disintegration rate is 5000 disintegrations per minute and after 5 minutes, the rate is 1250 disintegrations per minute.
A0.4ln2B0.2ln2C0.1ln2D0.8ln2A radioactive sample had an initial activity of 56 dpm . After 69.3 minutes, it was found to have an activity of 28 dpm . Find the number of atoms in a sample having an activity of 100 dpm.
A693B100C1000D10000
The disintegration rate of a certain radioactive sample at any instant is 4750 disintegrations per minute. Five minutes later the rate becomes 2700 per minute. Calculate
(a) decay constant and (b) half-life of the sample
View SolutionThe disintegration rate of a certain radioactive sample at any instant is 4750 disintegrations per minute. Five minutes later the rate becomes 2700 per minute. Calculate
(a) decay constant and (b) half-life of the sample
View SolutionThe disintegration rate of a certain radioactive sample at any instant is 4750 disintegrations per minute. Five minutes later the rate becomes 2700 per minute. Calculate
(a) decay constant and (b) half-life of the sample
View SolutionTwo radioactive substances X and Y initially contain equal number of atoms. Their half-lives are 1 hour and 2 hours respectively. Calculate the ratio of their rates of disintegration after four hours.
View SolutionThe radioactive sources A and B of half lives of t hr and 2t hr respectively, initially contain the same number of radioactive atoms. At the end of t hours, their rates of disintegration are in the ratio:
View Solution
