The ratio of the number of atoms of two radioactive elements A and B, in equilibrium with each other, is 3.1×109:1. If t12 of element B is 6.45 yrs, calculate that of element A.
To solve the problem, we need to find the half-life of element A given the ratio of the number of atoms of elements A and B in equilibrium and the half-life of element B.
1. Understand the Given Ratio:
The ratio of the number of atoms of elements A and B in equilibrium is given as:
NANB=3.1×109:1
This means:
NA=3.1×109⋅NB
2. Use the Relationship of Half-Lives:
In radioactive decay, the relationship between the number of atoms and half-lives of two radioactive elements in equilibrium is given by:
NANB=T1/2,BT1/2,A
Rearranging this gives us:
T1/2,AT1/2,B=NBNA
3. Substituting Known Values:
We know T1/2,B=6.45 years. Now substituting the values:
T1/2,A6.45=13.1×109
4. Calculate T1/2,A:
Rearranging gives:
T1/2,A=6.45⋅13.1×109
Calculating this:
T1/2,A=6.453.1×109≈2.08×10−9 years
5. Final Answer:
Therefore, the half-life of element A is approximately:
T1/2,A≈2.08×10−9 years
The ratio of the number of atoms of elements A and B in equilibrium is given as:
NANB=3.1×109:1
This means:
NA=3.1×109⋅NB
In radioactive decay, the relationship between the number of atoms and half-lives of two radioactive elements in equilibrium is given by:
NANB=T1/2,BT1/2,A
Rearranging this gives us:
T1/2,AT1/2,B=NBNA
We know T1/2,B=6.45 years. Now substituting the values:
T1/2,A6.45=13.1×109
Rearranging gives:
T1/2,A=6.45⋅13.1×109
Calculating this:
T1/2,A=6.453.1×109≈2.08×10−9 years
Therefore, the half-life of element A is approximately:
T1/2,A≈2.08×10−9 years
Topper's Solved these Questions
- ATOMIC STRUCTURE AND RADIOACTIVITYBOOK - RC MUKHERJEECHAPTER - ATOMIC STRUCTURE AND RADIOACTIVITYEXERCISE - Objective Problems
66 Videos
- ATOMIC STRUCTURE AND RADIOACTIVITYBOOK - RC MUKHERJEECHAPTER - ATOMIC STRUCTURE AND RADIOACTIVITYEXERCISE - Objective Problems
66 Videos
- ATOMIC WEIGHTBOOK - RC MUKHERJEECHAPTER - ATOMIC WEIGHTEXERCISE - PROBLEMS
6 Videos
Similar Questions
The ratio of the atoms of two elements A and B at radioactive equilibrium is 5.0×105 : 1 respectively. Calculate half life of B if half life of A is 245 days.
View SolutionAt radioactive equilibrium, the ratio between two atoms of radioactive elements A and B is 3.1×109:1. If the half-life period of A is 2×1010 years, what is the half-life of B?
View Solution
Knowledge Check
The graph between number of decayed atoms N' of a radioactive element and time t is.
A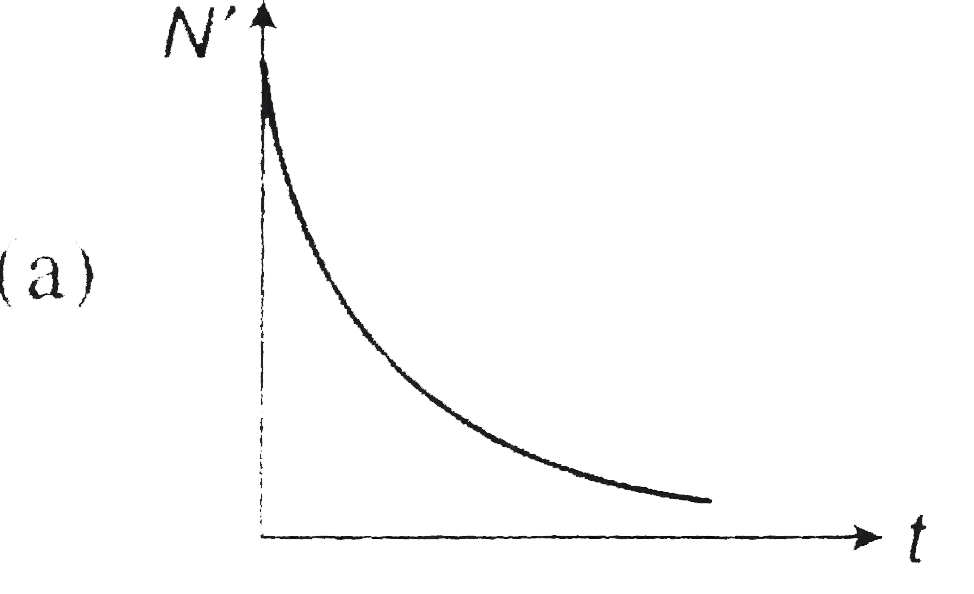 .B
.B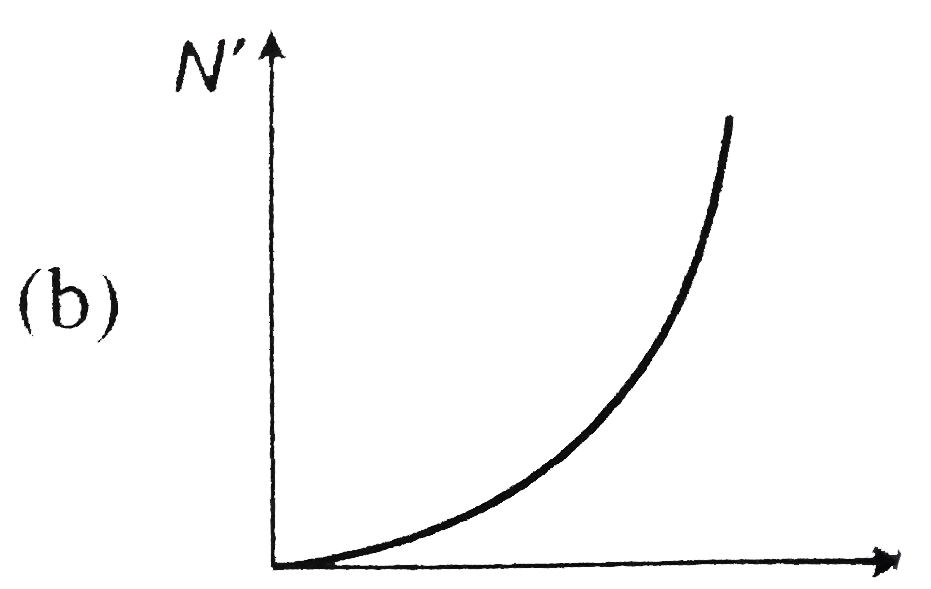 .C
.C .D
.D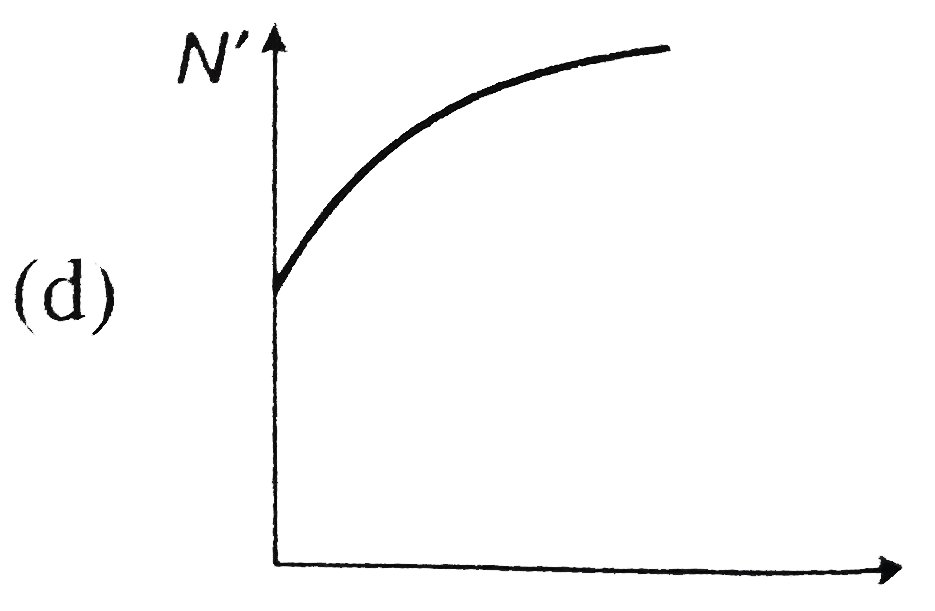 .
.The ratio of the amount of two element X and Y at radioactive equilibrium is 1:2×10−6. If the half-life period of element Y is 4.9×10−4 days, then the half-life period of element X will be
A4.8×10−3 daysB245 daysC122.5 daysDNone of theseThe wt. in g of 1 curie of a radioactive element 200X having t1/2 of 69.3 min is
A3.7×10−8 gB200 gC7.4×10−8gD3.0×10−8g
In a system in which two radioisotopes A and B are in equilibrium and ratio NA/NB is 4.0times10^(5). If t1/2 of A is 4times10^(6) years,then calculate the t1/2 for "B" ,(in years) "
View Solution3.011×1022 atoms of an element weighs 1.15gm. The atomic mass of the element is :
View Solution3.011×1022 atoms of an element weight 1.15 g. The atomic mass of the element is :-
View SolutionAn atom of an element weighs 6.644×10−23 g. Calculate g atoms of element in 40 kg-
View SolutionThe decay constant of a radioactive element is 3×10−6min−1. Its half-life is
View Solution