The molecular velocity of any gas is
inversely proportional to the square root of temperature
inversely proportional to absolute temperature
directly proportional to square of temperature
directly proportional to square root of temperature.
The correct Answer is:D
To solve the question regarding the molecular velocity of any gas, we will follow these steps:
1. Understanding Molecular Velocity:
- Molecular velocity refers to the speed of gas particles as they move in random motion. According to the kinetic molecular theory, gas particles are in constant random motion and collide with each other and the walls of their container.
2. Definition of Root Mean Square Speed (Vrms):
- The molecular velocity can be described using the root mean square speed (Vrms), which is a measure of the average velocity of gas particles. It accounts for the different speeds and directions of the particles.
3. Kinetic Energy Relation:
- The average kinetic energy of gas particles is given by the equation:
KE=32kBT
where kB is the Boltzmann constant and T is the absolute temperature.
4. Relating Kinetic Energy to Velocity:
- Kinetic energy can also be expressed in terms of mass and velocity:
KE=12mv2
- Setting these two expressions for kinetic energy equal gives:
32kBT=12mv2
5. Deriving the Expression for Vrms:
- Rearranging the equation gives:
v2=3kBTm
- Taking the square root, we find the root mean square speed:
Vrms=√3kBTm
6. Using Ideal Gas Constant:
- We can relate the Boltzmann constant to the ideal gas constant R and Avogadro's number NA:
kB=RNA
- Substituting this into the equation for Vrms:
Vrms=√3RTM
- Here, M is the molar mass of the gas.
7. Analyzing the Options:
- The derived equation shows that Vrms is directly proportional to the square root of the temperature T. Thus, we can conclude that:
- It is not inversely proportional to temperature.
- It is not proportional to the square of temperature.
- It is correct that it is directly proportional to the square root of temperature.
8. Conclusion:
- The correct answer is that the molecular velocity of any gas is directly proportional to the square root of the temperature.
Final Answer:
The molecular velocity of any gas is directly proportional to the square root of the temperature.
---
- Molecular velocity refers to the speed of gas particles as they move in random motion. According to the kinetic molecular theory, gas particles are in constant random motion and collide with each other and the walls of their container.
- The molecular velocity can be described using the root mean square speed (Vrms), which is a measure of the average velocity of gas particles. It accounts for the different speeds and directions of the particles.
- The average kinetic energy of gas particles is given by the equation:
KE=32kBT
where kB is the Boltzmann constant and T is the absolute temperature.
- Kinetic energy can also be expressed in terms of mass and velocity:
KE=12mv2
- Setting these two expressions for kinetic energy equal gives:
32kBT=12mv2
- Rearranging the equation gives:
v2=3kBTm
- Taking the square root, we find the root mean square speed:
Vrms=√3kBTm
- We can relate the Boltzmann constant to the ideal gas constant R and Avogadro's number NA:
kB=RNA
- Substituting this into the equation for Vrms:
Vrms=√3RTM
- Here, M is the molar mass of the gas.
- The derived equation shows that Vrms is directly proportional to the square root of the temperature T. Thus, we can conclude that:
- It is not inversely proportional to temperature.
- It is not proportional to the square of temperature.
- It is correct that it is directly proportional to the square root of temperature.
- The correct answer is that the molecular velocity of any gas is directly proportional to the square root of the temperature.
The molecular velocity of any gas is directly proportional to the square root of the temperature.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - TRUE OR FALSE TYPE QUESTION15videos
STATES OF MATTER : GASES AND LIQUIDS
- BOOK - ICSECHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - FILL IN THE BLANKS. TYPE QUESTIONS10videos
STATES OF MATTER : GASES AND LIQUIDS
- BOOK - ICSECHAPTER - STATES OF MATTER : GASES AND LIQUIDSEXERCISE - ESSAY (LONG ANSWER ) TYPE QUESTIONS10videos
STATES OF MATTER : GASES AND LIQUIDS
- BOOK - ICSECHAPTER - SOME P-BLOCK ELEMENTS EXERCISE - NCERT TEXTBOOK EXERCISES (With Hints and Solutions)63videos
SOME P-BLOCK ELEMENTS
- BOOK - ICSECHAPTER - STRUCTURE OF ATOMEXERCISE - NCERT Textbook Exercises67videos
STRUCTURE OF ATOM
Similar Questions
Knowledge Check
- Question 1 - Select One
8.2 L of an ideal gas weights 9.0 g at 300 K and 1 atm pressure. The molecular mass of the gas is
A54B27C13.5D81
The distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
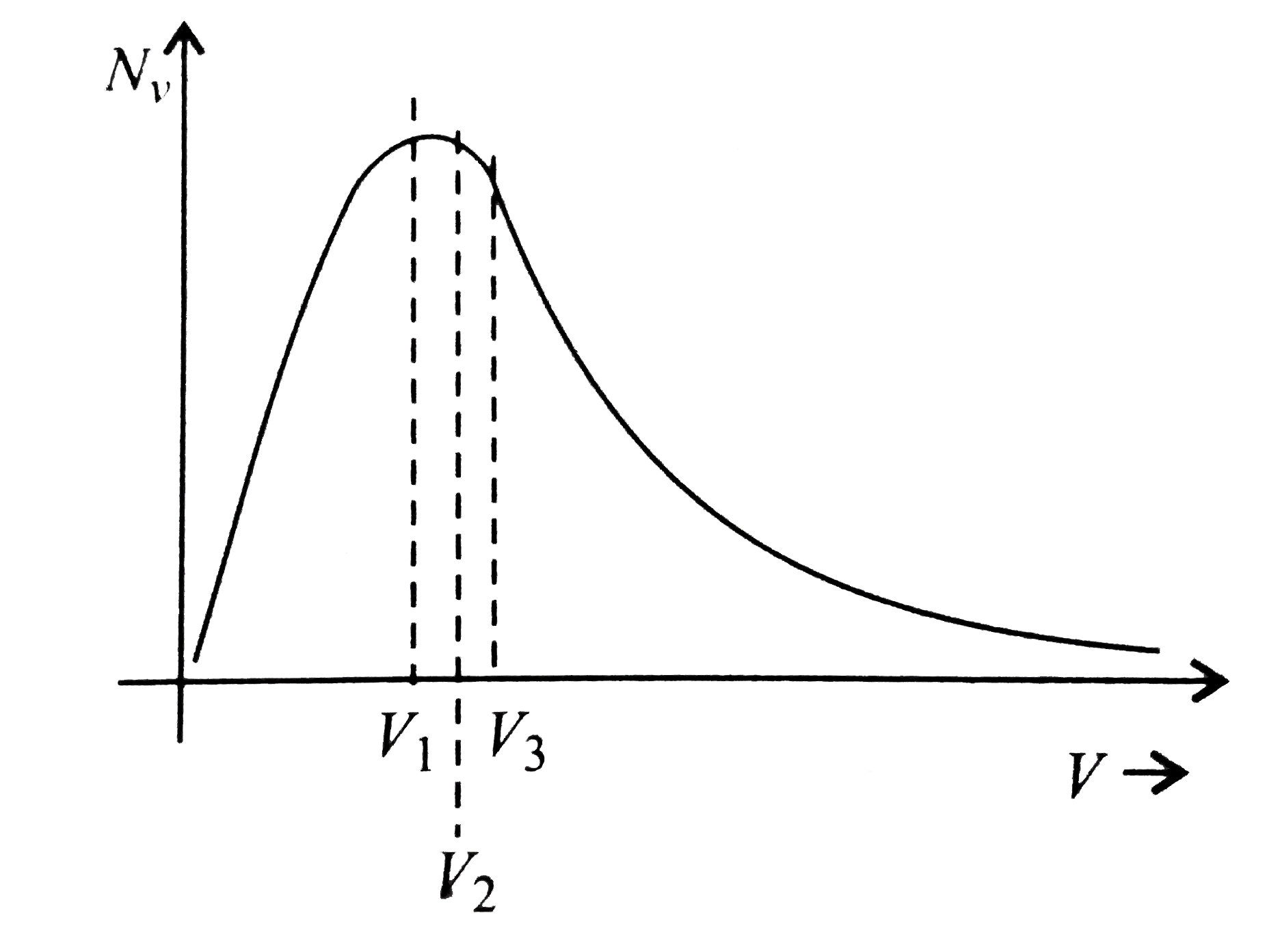
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of a areView SolutionThe distribution of the molecular velocities of gas molecules at any temperature T is shown below. (The plot below is known as Maxwell's distribution of molecular speeds.)
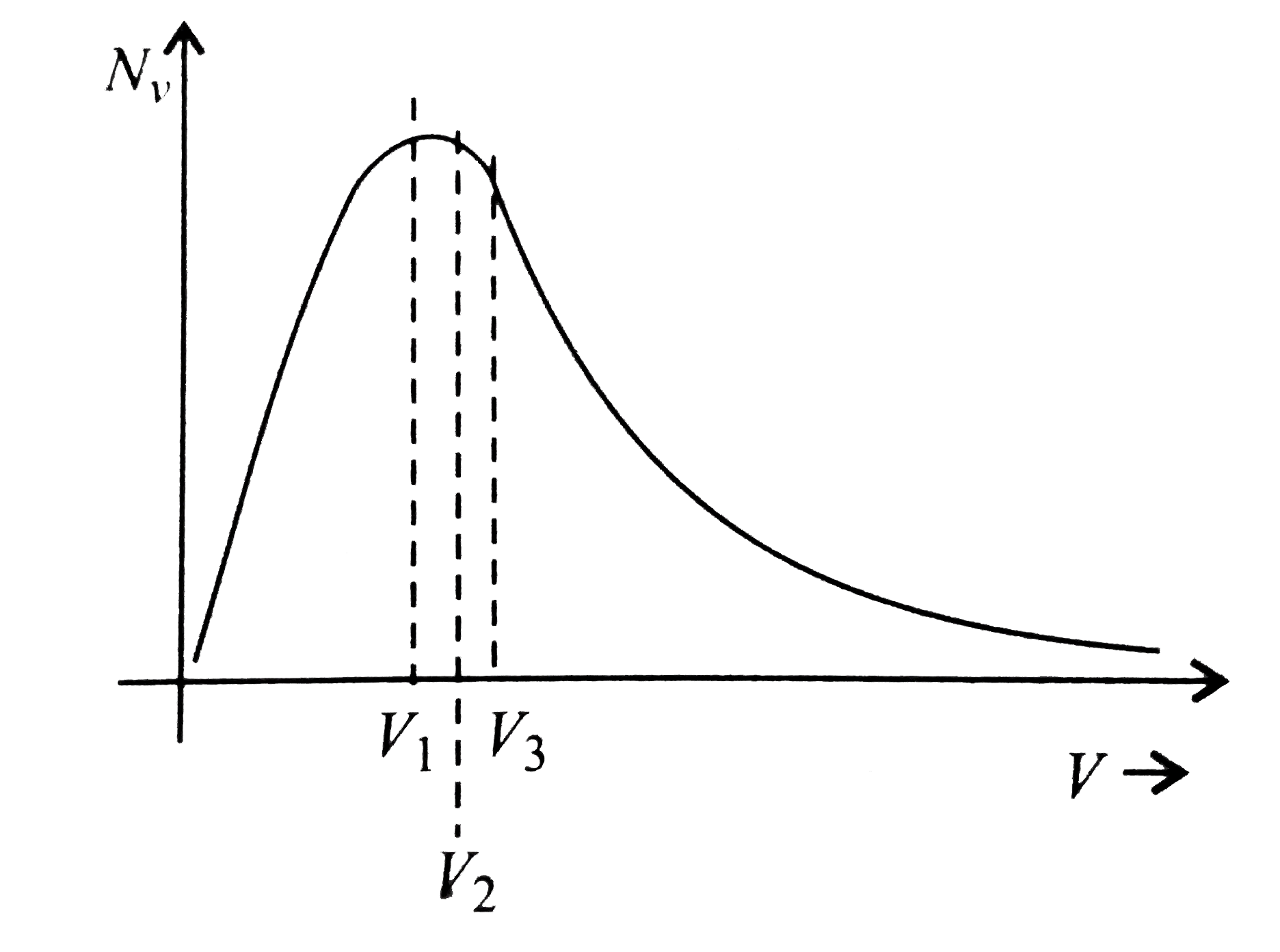
where
v is molecular velocity
n is number of molecules having velocity v
Let us define ΔNv, which is equal to the number of molecules between the velocity range v and v+Δv, given by
ΔNv=4πNa3e−bv2v2Δv
where
N is total number of molecules
a=√M02πRT and b=M02RT
R is universal gas constant
T is temperature of the gas
M0 is molecular weight of the gas
Answer the following question:
SI units of b areView SolutionAt 400K,the root mean square (rms) speed of a gas X (molecular weight=40) is equal to the most probable speed of gas Y at 60K . The molecular weight of the gas Y is :
View SolutionCalculate the molecular weight of a gas which diffuses four times as fast as another gas Y, which in turn diffuses twice as fast as another gas Z [All under identical conditions]. Molecules weight of Z is 128.
View SolutionCalculate the molecular weight of a gas X which diffuses four times as fast as another gas Y, which in turn diffuses twice as fast as another Z. Molecular weight of the gas Z is 128.
View SolutionFind the molecular weight for a gas in which the velocity of sound is 1260ms at 0∘C and whose γ is 1.4.
View SolutionFind the molecular weight for a gas in which the velocity of sound is 1260ms at 0∘C and whose γ is 1.4.
View Solution

