In isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that :
(i)
(ii)
(iii)
The correct Answer is:(i)
To prove the statements regarding the isosceles triangle ABC, we will follow a systematic approach using geometric properties and the Pythagorean theorem.
1. Draw the Triangle and Points:
- Draw triangle ABC where AB = AC (isosceles triangle).
- Let D be a point on the base BC and E be a point on the extension of BC beyond C.
2. Identify the Perpendicular:
- Draw a perpendicular line from point A to line BC, meeting at point F. This will help in applying the Pythagorean theorem.
3. Establish Equal Segments:
- Since triangle ABC is isosceles, the perpendicular from A to BC bisects BC at point F. Therefore, we have BF = FC.
4. Apply Pythagorean Theorem in Triangle AFB:
- In triangle AFB, by the Pythagorean theorem:
AB2=AF2+BF2(1)
5. Apply Pythagorean Theorem in Triangle AFD:
- In triangle AFD, we have:
AD2=AF2+DF2(2)
6. Apply Pythagorean Theorem in Triangle ACF:
- In triangle ACF, we have:
AC2=AF2+CF2(3)
- Since BF = FC, we can substitute CF with BF in equation (3):
AC2=AF2+BF2
7. Compare AC and AD:
- From equations (1) and (2), since BF > DF (D is between B and C), we can conclude:
AC2>AD2⟹AC>AD(4)
8. Apply Pythagorean Theorem in Triangle AFE:
- In triangle AFE, we have:
AE2=AF2+EF2(5)
- Since E lies on the extension of BC, EF > BF.
9. Compare AE and AC:
- From equations (3) and (5), since EF > BF:
AE2>AC2⟹AE>AC(6)
10. Compare AE and AD:
- Since EF > DF (E is beyond D on line BC):
AE2>AD2⟹AE>AD(7)
Conclusion
From the above steps, we have proven:
1. AC>AD
2. AE>AC
3. AE>AD
- Draw triangle ABC where AB = AC (isosceles triangle).
- Let D be a point on the base BC and E be a point on the extension of BC beyond C.
- Draw a perpendicular line from point A to line BC, meeting at point F. This will help in applying the Pythagorean theorem.
- Since triangle ABC is isosceles, the perpendicular from A to BC bisects BC at point F. Therefore, we have BF = FC.
- In triangle AFB, by the Pythagorean theorem:
AB2=AF2+BF2(1)
- In triangle AFD, we have:
AD2=AF2+DF2(2)
- In triangle ACF, we have:
AC2=AF2+CF2(3)
- Since BF = FC, we can substitute CF with BF in equation (3):
AC2=AF2+BF2
- From equations (1) and (2), since BF > DF (D is between B and C), we can conclude:
AC2>AD2⟹AC>AD(4)
- In triangle AFE, we have:
AE2=AF2+EF2(5)
- Since E lies on the extension of BC, EF > BF.
- From equations (3) and (5), since EF > BF:
AE2>AC2⟹AE>AC(6)
- Since EF > DF (E is beyond D on line BC):
AE2>AD2⟹AE>AD(7)
From the above steps, we have proven:
1. AC>AD
2. AE>AC
3. AE>AD
Topper's Solved these Questions
Similar Questions
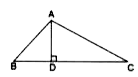
From the following figure, prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
View SolutionFind :
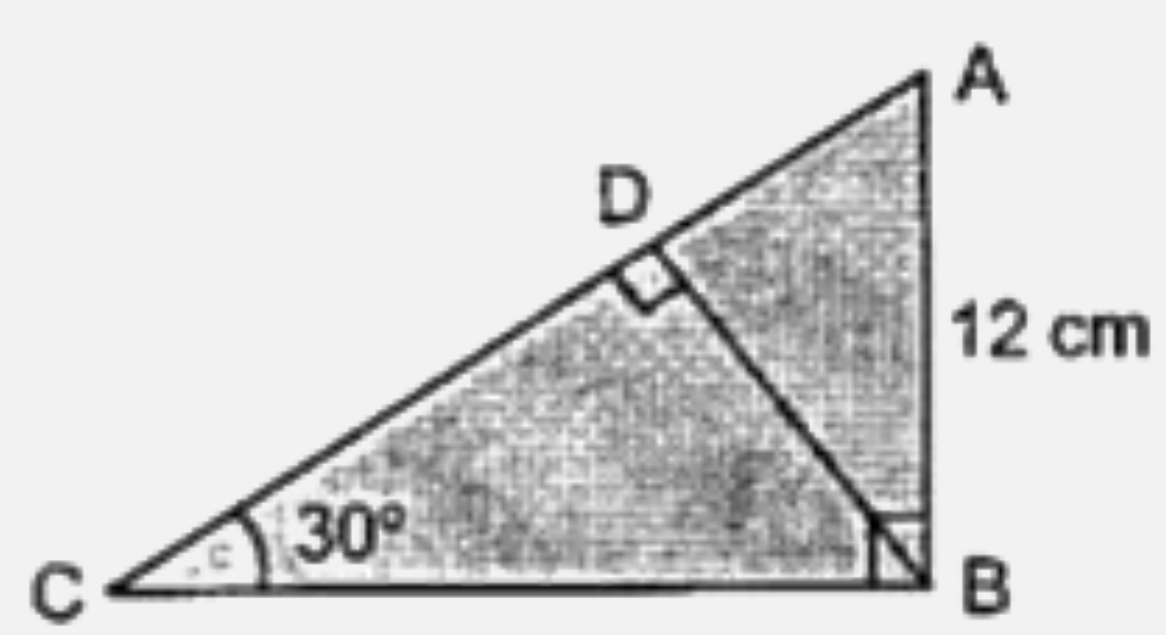
(i) BC
(ii) AD
(iii) AC
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.

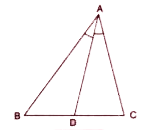
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC

View SolutionIn a quadrilateral ABCD, prove that :
(i) AB+BC+CD>DA
(ii) AB+BC+CD+DA>2AC
(iii) AB+BC+CD+DA>2BD
View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If AD⊥BC, find the length of AD .
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that :
AD2=AC2+BD.CD
View Solution
