In a quadrilateral ABCD, prove that :
(i) AB+BC+CD>DA
(ii) AB+BC+CD+DA>2AC
(iii) AB+BC+CD+DA>2BD
Step by step video & image solution for In a quadrilateral ABCD, prove that : (i) AB+BC+CD gt DA (ii) AB+BC+CD+DA gt 2AC (iii) AB+BC+CD+DA gt 2BD by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD

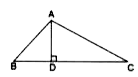
View SolutionFrom the following figure, prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
View SolutionAD is a median of triangle ABC. Prove that : AB+BC+AC>2AD
View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA>AC+BD
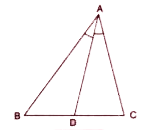
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC

View SolutionShow that in a quadrilateral ABCD AB+BC+CD+DA<2(BD+AC)
View SolutionIn isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that :
(i) AC>AD
(ii) AE>AC
(iii) AE>AD
View SolutionIn the given figure AC = BD, prove that AB = CD.

View SolutionIn a quadrilateral ABCD, AB = CD and ∠B=∠C. Prove that
AC=AB
View Solution
