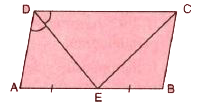
Draw parallelogram ABCD with the following data :
.
Let AC and DB in O let E be the mid-point of BC. Join OE. Prove that :
(i)
(ii) .
Step-by-Step Solution:
1. Draw Line Segment AB:
- Start by drawing a horizontal line segment AB that measures 6 cm. Label the endpoints as A and B.
Hint: Use a ruler to ensure that the line segment is exactly 6 cm long.
2. Construct Angle DAB:
- At point A, construct an angle of 45 degrees. To do this, first draw a perpendicular line (90 degrees) to AB at point A. Then, bisect this angle to get 45 degrees.
Hint: You can use a compass to mark arcs and find the intersection point to help bisect the angle accurately.
3. Locate Point D:
- From point A, measure 5 cm along the line you just created at 45 degrees to locate point D.
Hint: Use the compass to measure 5 cm from point A to ensure accuracy.
4. Locate Point C:
- Since ABCD is a parallelogram, we know that AB is parallel to DC and AD is parallel to BC. From point B, draw an arc of 5 cm to find point C. From point D, draw an arc of 6 cm to find point C as well. The intersection of these two arcs will give you point C.
Hint: Make sure to keep your compass at the same width while drawing arcs from points B and D.
5. Complete the Parallelogram:
- Connect points B to C and D to C to complete the parallelogram ABCD.
Hint: Double-check that opposite sides are equal in length to confirm that you have constructed a parallelogram.
6. Identify Midpoints and Join OE:
- Let O be the intersection point of diagonals AC and BD. Find the midpoint E of line segment BC. Join points O and E.
Hint: To find the midpoint E, measure the length of BC and divide it by 2, then mark the midpoint.
7. Prove that OE is Parallel to AB:
- According to the Midpoint Theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length. Since O is the midpoint of AC and E is the midpoint of BC, OE is parallel to AB.
Hint: Remember that the Midpoint Theorem applies here because you are working with triangle ABC.
8. Prove that OE = (1/2) AB:
- Since OE is parallel to AB and by the Midpoint Theorem, OE is half the length of AB. Therefore, OE = 1/2 * AB = 1/2 * 6 cm = 3 cm.
Hint: Measure OE with a ruler to confirm that it is indeed 3 cm, which should match your calculation.
- Start by drawing a horizontal line segment AB that measures 6 cm. Label the endpoints as A and B.
- At point A, construct an angle of 45 degrees. To do this, first draw a perpendicular line (90 degrees) to AB at point A. Then, bisect this angle to get 45 degrees.
- From point A, measure 5 cm along the line you just created at 45 degrees to locate point D.
- Since ABCD is a parallelogram, we know that AB is parallel to DC and AD is parallel to BC. From point B, draw an arc of 5 cm to find point C. From point D, draw an arc of 6 cm to find point C as well. The intersection of these two arcs will give you point C.
- Connect points B to C and D to C to complete the parallelogram ABCD.
- Let O be the intersection point of diagonals AC and BD. Find the midpoint E of line segment BC. Join points O and E.
- According to the Midpoint Theorem, the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length. Since O is the midpoint of AC and E is the midpoint of BC, OE is parallel to AB.
- Since OE is parallel to AB and by the Midpoint Theorem, OE is half the length of AB. Therefore, OE = 1/2 * AB = 1/2 * 6 cm = 3 cm.
Topper's Solved these Questions
Similar Questions
Constructed a parallelogram ABCD, when :
AB=6.0cm,AD=5.0cmand∠A=45∘
View SolutionUsing ruler and compasses only, construct a parallelogram ABCD, using the following data: AB=6cm,AD=3cmand∠DAB=45∘. If the bisector of ∠DAB meets DC at P, prove that ∠APB is a right angle.
View SolutionConstructed a parallelogram ABCD, when :
AB=4.4cm,AD=6.2cmandAC=4.8cm.
View SolutionConstruct a quadrilateral ABCD, when :
AD=AB=4cm,BC=2.8cm,CD=2.5cmand angleBAD=45∘.
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
BC= BE
View SolutionABCD is trapezium in which AB∣∣DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
ar(DCYX)=79ar(XYBA).
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionConstructed a parallelogram ABCD, when :
AB=5.8cm, diagonal AC=8.2cm and diagonal BD=6.2cm.
View SolutionDraw a parallelogram ABCD, with AB=6cm, AD=4.8 cm and ∠DAB=45∘.
Draw the perpendicular bisector of side AD and let it meet AD at point P. also, draw the diagonals AC and BD, and let them intersect at point O. join O and P. measure OP. DC=5 cm
View SolutionConstruct a trapezium ABCD, when :
AB=CD=3.2cm,BC=6.0cm,AD=4.4cmandAD/BC.
View Solution