In parallelogram ABCD, P is a point on side AB and Q is a ponit on side BC.
Prove that :
(i) ΔCPD and ΔAQD are equal in area.
(ii) Area (ΔAQD)
=Area(ΔAPD)+Area(ΔCPB)
To solve the problem, we will prove the two statements step by step.
Given:
- Parallelogram ABCD
- Point P on side AB
- Point Q on side BC
To Prove:
1. Area of triangle CPD = Area of triangle AQD
2. Area of triangle AQD = Area of triangle APD + Area of triangle CPB
Step 1: Prove that Area of triangle CPD = Area of triangle AQD
Proof:
1. Identify the bases and heights:
- Triangle CPD and parallelogram ABCD share the base CD and are between the same parallel lines AB and CD.
- Triangle AQD and parallelogram ABCD share the base AD and are between the same parallel lines AD and BC.
2. Apply the area theorem:
- According to the theorem, the area of a triangle on the same base and between the same parallel lines is half the area of the parallelogram.
- Therefore, we can write:
Area of △CPD=12×Area of parallelogram ABCD \quad (1)
- Similarly,
Area of △AQD=12×Area of parallelogram ABCD \quad (2)
3. Equate the two areas:
- From equations (1) and (2), since both are equal to half the area of the same parallelogram, we have:
Area of △CPD=Area of △AQD
- Hence, the first part is proved.
Step 2: Prove that Area of triangle AQD = Area of triangle APD + Area of triangle CPB
Proof:
1. Express the area of parallelogram ABCD:
- The area of parallelogram ABCD can be expressed as the sum of the areas of triangles APD, CPD, and CPB:
Area of parallelogram ABCD=Area of △APD+Area of △CPD+Area of △CPB(3)
2. Substitute the area of parallelogram from part 1:
- From the first part, we know that:
Area of parallelogram ABCD=Area of △CPD+Area of △AQD(4)
3. Set equations (3) and (4) equal:
- From (3) and (4), we can equate:
Area of △APD+Area of △CPD+Area of △CPB=Area of △CPD+Area of △AQD
4. Cancel the common area of triangle CPD:
- By subtracting the area of triangle CPD from both sides:
Area of △APD+Area of △CPB=Area of △AQD
- Hence, we have proved the second part.
Final Result:
1. Area of triangle CPD = Area of triangle AQD
2. Area of triangle AQD = Area of triangle APD + Area of triangle CPB
---
- Parallelogram ABCD
- Point P on side AB
- Point Q on side BC
1. Area of triangle CPD = Area of triangle AQD
2. Area of triangle AQD = Area of triangle APD + Area of triangle CPB
- Triangle CPD and parallelogram ABCD share the base CD and are between the same parallel lines AB and CD.
- Triangle AQD and parallelogram ABCD share the base AD and are between the same parallel lines AD and BC.
- According to the theorem, the area of a triangle on the same base and between the same parallel lines is half the area of the parallelogram.
- Therefore, we can write:
Area of △CPD=12×Area of parallelogram ABCD \quad (1)
- Similarly,
Area of △AQD=12×Area of parallelogram ABCD \quad (2)
- From equations (1) and (2), since both are equal to half the area of the same parallelogram, we have:
Area of △CPD=Area of △AQD
- Hence, the first part is proved.
- The area of parallelogram ABCD can be expressed as the sum of the areas of triangles APD, CPD, and CPB:
Area of parallelogram ABCD=Area of △APD+Area of △CPD+Area of △CPB(3)
- From the first part, we know that:
Area of parallelogram ABCD=Area of △CPD+Area of △AQD(4)
- From (3) and (4), we can equate:
Area of △APD+Area of △CPD+Area of △CPB=Area of △CPD+Area of △AQD
- By subtracting the area of triangle CPD from both sides:
Area of △APD+Area of △CPB=Area of △AQD
- Hence, we have proved the second part.
1. Area of triangle CPD = Area of triangle AQD
2. Area of triangle AQD = Area of triangle APD + Area of triangle CPB
Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
In a parallelogram ABCD, P is a point on side AD such that 3AP = AD and Q is a point on BC such that 3CQ = BC. Prove that : AQCP is a parallelogram.
View SolutionIn trapezium ABCD, side AB is parallel to side DC. Diagonals AC and BD intersect at point P. Prove that triangles APD and BPC are equal in area.
View SolutionIn parallelogram ABCD, points P and Q lie on side BC and trisect it. Prove that :
ar.(ΔAPQ)=ar.(ΔDPQ)
=16×ar. (Parallelogram ABCD)
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔACD)= area (ΔABE)
View SolutionIn parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B.
Prove that P is equidistant from AB and BC.
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔOBD)= area (ΔOCE)
View SolutionO' is an interior point of a parallelogram ABCD. Prove that :
area of ΔAOB+ area of ΔCOD= area of ΔAOD+ area of ΔBOC
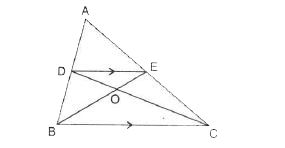
View SolutionIn the following figure, DE is parallel to BC. Show that :
(i) Area(ΔADC)=Area(ΔAEB)
(ii) Area(ΔBOD)=Area(ΔCOE).
View SolutionP is any point inside a parallelogram ABCD. Prove that :
Area (ΔAPB)+Area(ΔCPD)
=Area(ΔAPD)+Area(ΔBPC)
View SolutionIn parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of ΔPOB=40cm2 and OP:OC= 1:2, find :
(i) Areas of ΔBOC and ΔPBC
(ii) Areas of ΔABC and parallelogram ABCD.
View Solution