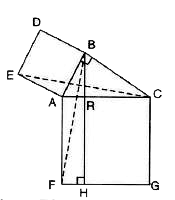
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
If BH perpendicular to FG, prove that :
(i) ΔEAC≅ΔBAF.
(ii) Area of the square ABDE
= Area of the rectangle ARHF.
Step by step video & image solution for In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC. If BH perpendicular to FG, prove that : (i) DeltaEAC~=DeltaBAF. (ii) Area of the square ABDE = Area of the rectangle ARHF. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
ABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC. Prove that :

(i) ΔADE~ΔACB.
View SolutionOn the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
∠CAD=∠BAE
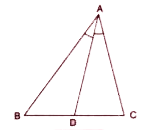
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
View SolutionIn the figure, given alongside, AD bisects angle BAC. Prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC

View SolutionOn the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
(i) ∠CAD=∠BAE
(ii) CD = BE
View SolutionEquilateral triangles ABD and ACE are drawn on sides AB and AC respectively of a ΔABC outside it. Prove that :
(i) ∠DAC=∠EAB (ii) DC=BE
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

Find, area of AADE: area of quadrilateral BCED.
View SolutionThe given figure shows a parallelogram ABCD. Squares ABPQ and ADRS are drawn on sides AB and AD of the parallelogram ABCD. Prove that :
(i) ∠SAQ=∠ABC
(ii) SQ = AC

View SolutionIn a right triangle ABC, right angled at A, AD is drawn perpendicular to BC. Prove that:
AB2−BD2=AC2−CD2
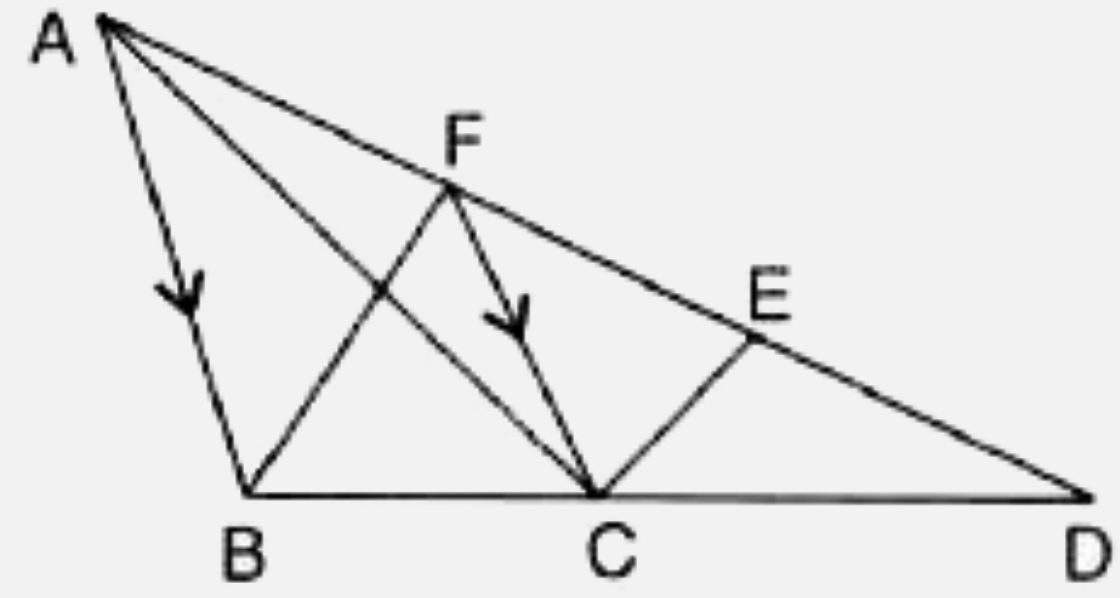
View SolutionIn the following figure, F and E are points on the side AD of the triangle ABD. Through F a line is drawn parallel to AB to meet BD at point C .
Prove that : ar (ΔACE)=ar (quad . BCEF )
View Solution
