Given : CP is bisector of angle C of ΔABC.

Prove : P is equidistant from AC and BC.
Step by step video & image solution for Given : CP is bisector of angle C of DeltaABC. Prove : P is equidistant from AC and BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LOCI (LOCUS AND ITS CONSTRUCTIONS)BOOK - ICSECHAPTER - LOCI (LOCUS AND ITS CONSTRUCTIONS)EXERCISE - EXERCISE 16(B)
49 Videos
- LOCI (LOCUS AND ITS CONSTRUCTIONS)BOOK - ICSECHAPTER - LOCI (LOCUS AND ITS CONSTRUCTIONS)EXERCISE - EXERCISE 16(B)
49 Videos
- LINEAR INEQUATIONSBOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Competency Based Questions
15 Videos
- MATHEMATICS -2014BOOK - ICSECHAPTER - MATHEMATICS -2014EXERCISE - SECTION- B
29 Videos
Similar Questions
In triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
F is equidistant from AB and BC.
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
E is equidistant from A and B
View SolutionIn parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B.
Prove that P is equidistant from AB and BC.
View SolutionConstruct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
View SolutionConstruct a triangle ABC which angle ABC=75∘,AB=5 cmandBC=6.4 cm. Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisector intersect each other at point P, prove that P is equidistant from B and C, and also from AC and BC.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Δ ABC. Prove that ∠PAC=∠BCAand□ABCP is a parallelogram.
View SolutionThe given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that : F is equidistant from AB and AC.
View SolutionIn the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that : point P is equidistant from A and B.
View SolutionIn the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that :
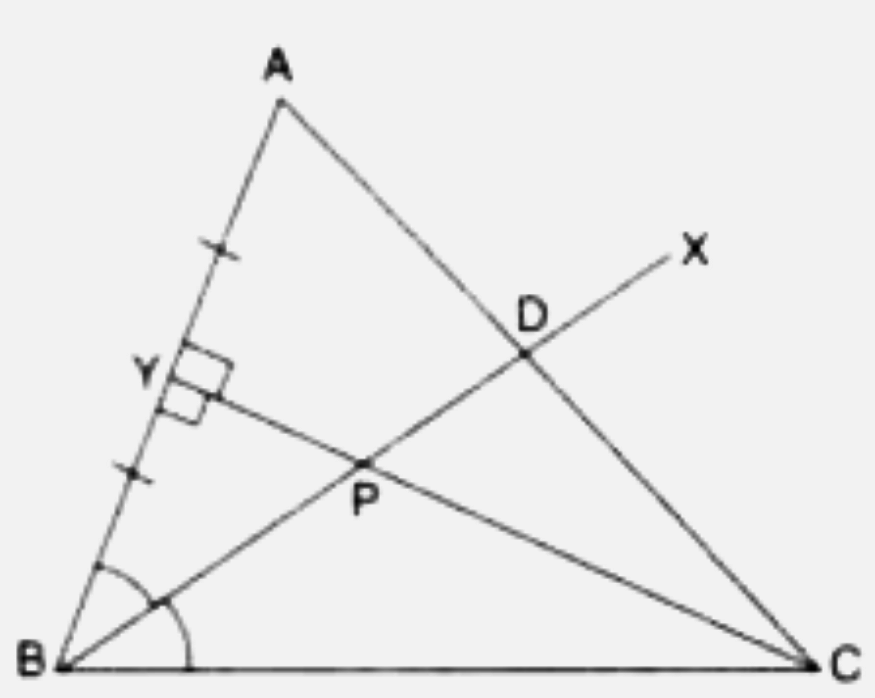
point D is equidistant from AB and BC.
View SolutionConstruct a triangle ABC, with AB = 6 cm, BC = 7 cm and ∠ABC=60∘ . Locate by construction the point P such that (i) P is equidistant from B and C (ii) P is equidistant from AB and BC. (iii) Measure and record the length of PA.
View Solution
