Given : AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.

Prove : Y is equidistant from A and C.
Step by step video & image solution for Given : AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y. Prove : Y is equidistant from A and C. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LOCI (LOCUS AND ITS CONSTRUCTIONS)BOOK - ICSECHAPTER - LOCI (LOCUS AND ITS CONSTRUCTIONS)EXERCISE - EXERCISE 16(B)
49 Videos
- LOCI (LOCUS AND ITS CONSTRUCTIONS)BOOK - ICSECHAPTER - LOCI (LOCUS AND ITS CONSTRUCTIONS)EXERCISE - EXERCISE 16(B)
49 Videos
- LINEAR INEQUATIONSBOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Competency Based Questions
15 Videos
- MATHEMATICS -2014BOOK - ICSECHAPTER - MATHEMATICS -2014EXERCISE - SECTION- B
29 Videos
Similar Questions
The given figure shows a triangle ABC in which AD bisects angle BAC. EG is perpendicular bisector of side AB which intersects AD at point F.
Prove that : F is equidistant from AB and AC.
View SolutionConstruct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
F is equidistant from AB and BC.
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
E is equidistant from A and B
View SolutionIn the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that : point P is equidistant from A and B.
View SolutionIn the figure, BX bisects angle ABC and intersects AC at point D. Line segment CY is perpendicular to AB and intersects BX at point P. If Y is mid-point of AB, prove that :
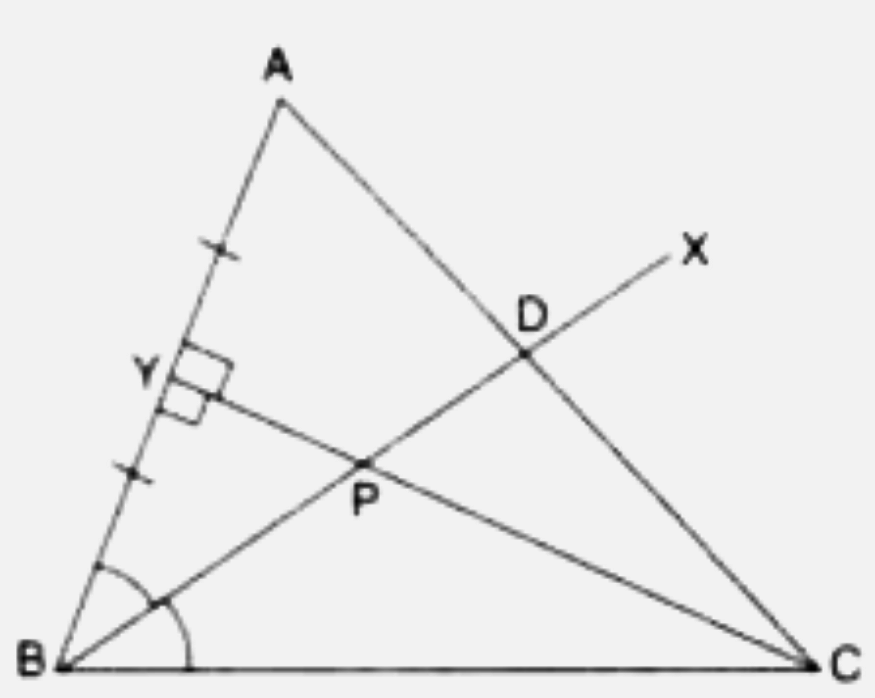
point D is equidistant from AB and BC.
View SolutionConstruct a triangle ABC which angle ABC=75∘,AB=5 cmandBC=6.4 cm. Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisector intersect each other at point P, prove that P is equidistant from B and C, and also from AC and BC.
View SolutionConstruct a right angled triangle PQR, in which ∠Q=90∘, hypotenuse PR =8 cm and QR = 4.5 cm. Draw bisector of angle PQR and let it meet PR at point T. Prove that T is equidistant from PQ and QR.
View SolutionIn parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B.
Prove that P is equidistant from AB and BC.
View SolutionIn each of the given figures, PA = PB and QA = QB.

Prove, in each case, that PQ (produce, if required) is perpendicular bisector of AB.
Hence, state the locus of the points equidistant from two given fixed points.
View Solution
