In the adjoining figure , ∠BCD=∠ADB (each 90∘) . angle BC= 3 cm and length of side opposite ∠C in ΔBCD is 5 cm , then find the squre root of length of side opposite to ∠D in ΔADB.
To solve the problem step by step, we will follow the given information and apply the Pythagorean theorem where necessary.
Step 1: Understand the problem
We have two triangles, ΔBCD and ΔADB, with the following information:
- Angle BCD = Angle ADB = 90 degrees
- BC = 3 cm
- The length of the side opposite angle C (BD) in ΔBCD = 5 cm
- We need to find the square root of the length of the side opposite angle D (AB) in ΔADB.
Step 2: Identify the sides in triangle BCD
In triangle BCD:
- BD is the hypotenuse = 5 cm
- BC is one of the sides = 3 cm
- We need to find CD using the Pythagorean theorem.
Step 3: Apply the Pythagorean theorem in triangle BCD
According to the Pythagorean theorem:
BD2=BC2+CD2
Substituting the known values:
52=32+CD2
25=9+CD2
CD2=25−9
CD2=16
Taking the square root:
CD=4 cm
Step 4: Establish relationships in triangle ADB
In triangle ADB:
- AD is the hypotenuse
- AE is the perpendicular from D to AB
- DE is the base = BC = 3 cm
- CD = BE = 4 cm (since CD = BE, as DE is parallel to BC)
Step 5: Set up the equation for triangle ADB
Using the Pythagorean theorem in triangle ADB:
AD2=AE2+DE2
Let AE = x cm, then:
AD2=x2+32
AD2=x2+9 (Equation 1)
Step 6: Set up the equation for triangle ABD
In triangle ABD:
- AB is the hypotenuse
- BD = 4 cm
Using the Pythagorean theorem:
AB2=AD2+BD2
Substituting the known values:
AB2=AD2+42
AB2=AD2+16 (Equation 2)
Step 7: Substitute Equation 1 into Equation 2
From Equation 1, we have:
AD2=x2+9
Substituting this into Equation 2:
AB2=(x2+9)+16
AB2=x2+25
Step 8: Express AB in terms of x
We know that:
AB=x+4
So:
(x+4)2=x2+25
Expanding the left side:
x2+8x+16=x2+25
Subtracting x2 from both sides:
8x+16=25
8x=25−16
8x=9
x=98=1.125 cm
Step 9: Find AB
Now substituting back to find AB:
AB=x+4=1.125+4=5.125 cm
Step 10: Find the square root of AB
Now we need to find the square root of AB:
√AB=√5.125
Calculating:
√5.125≈2.265 cm
Final Answer
The square root of the length of the side opposite to angle D in triangle ADB is approximately 2.265 cm.
We have two triangles, ΔBCD and ΔADB, with the following information:
- Angle BCD = Angle ADB = 90 degrees
- BC = 3 cm
- The length of the side opposite angle C (BD) in ΔBCD = 5 cm
- We need to find the square root of the length of the side opposite angle D (AB) in ΔADB.
In triangle BCD:
- BD is the hypotenuse = 5 cm
- BC is one of the sides = 3 cm
- We need to find CD using the Pythagorean theorem.
According to the Pythagorean theorem:
BD2=BC2+CD2
Substituting the known values:
52=32+CD2
25=9+CD2
CD2=25−9
CD2=16
Taking the square root:
CD=4 cm
In triangle ADB:
- AD is the hypotenuse
- AE is the perpendicular from D to AB
- DE is the base = BC = 3 cm
- CD = BE = 4 cm (since CD = BE, as DE is parallel to BC)
Using the Pythagorean theorem in triangle ADB:
AD2=AE2+DE2
Let AE = x cm, then:
AD2=x2+32
AD2=x2+9 (Equation 1)
In triangle ABD:
- AB is the hypotenuse
- BD = 4 cm
Using the Pythagorean theorem:
AB2=AD2+BD2
Substituting the known values:
AB2=AD2+42
AB2=AD2+16 (Equation 2)
From Equation 1, we have:
AD2=x2+9
Substituting this into Equation 2:
AB2=(x2+9)+16
AB2=x2+25
We know that:
AB=x+4
So:
(x+4)2=x2+25
Expanding the left side:
x2+8x+16=x2+25
Subtracting x2 from both sides:
8x+16=25
8x=25−16
8x=9
x=98=1.125 cm
Now substituting back to find AB:
AB=x+4=1.125+4=5.125 cm
Now we need to find the square root of AB:
√AB=√5.125
Calculating:
√5.125≈2.265 cm
The square root of the length of the side opposite to angle D in triangle ADB is approximately 2.265 cm.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Problems From NCERT/exemplar29videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Exercise 8a20videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 11 B10videos
CONSTRUCTIONS
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Revision Exercise Long Answer Questions8videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
In the adjoining figure :
Name the side opposite to ∠R
 View Solution
View SolutionIn the adjoining figure :
Name the angle opposite to side QR.
 View Solution
View SolutionIn the adjoining figure, AP=8cm, BP=2cm and ∠CPA=90∘. Find the length of chord CD.
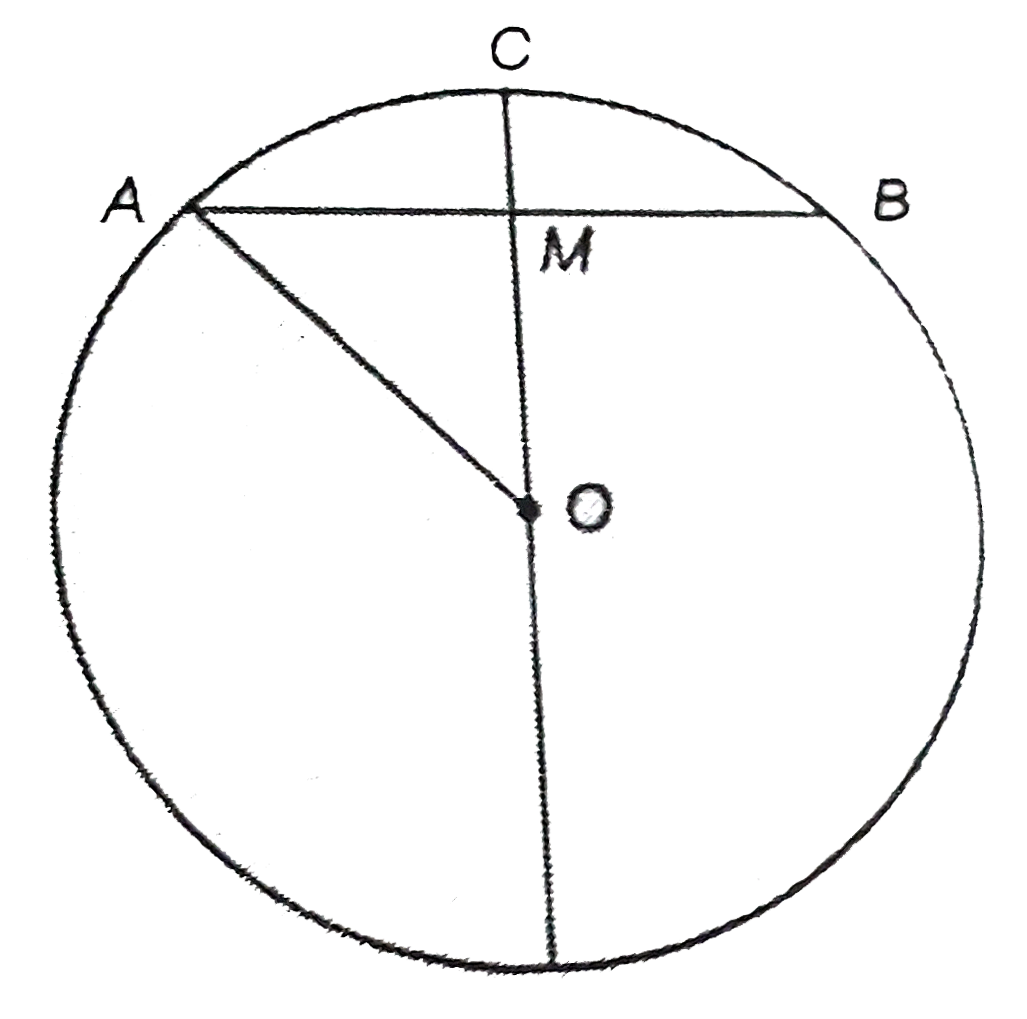 View Solution
View SolutionIn the adjoining figure, AB=8cm,DM=6cmandBC=6cm. Find the length of DN
 View Solution
View SolutionIn the adjoining figure: ∠PSQ=90∘ , PQ= 10 cm , QS = 6cm and RQ = 9cm . Calculate the length of PR.
View SolutionIn the following figure, ∠ABC=90∘ AB = (x+8) cm , BC = (x+ 1) cm and AC = (x+15) cm.
Find the lengths of the sides of the triangles.
 View Solution
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.
 View Solution
View SolutionIn the given figure, AB∣∣CD,AB=7cm,BD=25cmandCD=17cm, find the length of side BC.
 View Solution
View SolutionIf two sides of a tringle are of length 5 cm and 1.5 cm, then the length of third side of the triangle cannot be
View SolutionIn the given figure , ∠1=∠2and∠3=∠4. If BC= 7.5 cm , DE= 12.5cm and area of △ABC=13.5cm2 . Find the area of △ADE.
 View Solution
View Solution

