The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle . The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs 2.25 per m2
The correct Answer is:Rs 2002.61orRs2002.50
To solve the problem, we need to calculate the internal surface area of the railway tunnel (excluding the floor) and then find the cost of plastering that area. The tunnel has a rectangular cross-section with a semi-circle on top.
1. Identify the dimensions of the tunnel:
- The width of the rectangular part is 6 m.
- The height of the rectangular part is 8 m.
- The length of the tunnel is 35 m.
2. Calculate the radius of the semi-circle:
- The diameter of the semi-circle is equal to the width of the rectangle, which is 6 m.
- Therefore, the radius r of the semi-circle is:
r=62=3 m
3. Calculate the area of the semi-circle:
- The area A of a full circle is given by the formula A=πr2.
- The area of the semi-circle is half of that:
Area of semi-circle=12πr2=12×227×(32)=12×227×9=19814=997 m2
4. Calculate the curved surface area of the semi-circle along the length of the tunnel:
- The curved surface area (CSA) of the semi-circle is given by the formula CSA=perimeter of semi-circle×length.
- The perimeter of the semi-circle is πr:
Perimeter of semi-circle=πr=227×3=667 m
- Therefore, the curved surface area of the semi-circle over the length of the tunnel is:
CSA of semi-circle=667×35=23107=330 m2
5. Calculate the area of the rectangular sides:
- The area of the two rectangular sides (excluding the floor) is:
Area of two rectangles=2×height×length=2×8×35=560 m2
6. Calculate the total internal surface area (excluding the floor):
- The total internal surface area is the sum of the curved surface area of the semi-circle and the area of the two rectangular sides:
Total Surface Area=CSA of semi-circle+Area of two rectangles=330+560=890 m2
7. Calculate the cost of plastering:
- The cost of plastering is given as Rs 2.25 per m². Therefore, the total cost is:
Total Cost=Total Surface Area×Cost per m2=890×2.25=2002.50 Rs
Final Answer:
The cost of plastering the internal surface of the tunnel (excluding the floor) is Rs 2002.50.
- The width of the rectangular part is 6 m.
- The height of the rectangular part is 8 m.
- The length of the tunnel is 35 m.
- The diameter of the semi-circle is equal to the width of the rectangle, which is 6 m.
- Therefore, the radius r of the semi-circle is:
r=62=3 m
- The area A of a full circle is given by the formula A=πr2.
- The area of the semi-circle is half of that:
Area of semi-circle=12πr2=12×227×(32)=12×227×9=19814=997 m2
- The curved surface area (CSA) of the semi-circle is given by the formula CSA=perimeter of semi-circle×length.
- The perimeter of the semi-circle is πr:
Perimeter of semi-circle=πr=227×3=667 m
- Therefore, the curved surface area of the semi-circle over the length of the tunnel is:
CSA of semi-circle=667×35=23107=330 m2
- The area of the two rectangular sides (excluding the floor) is:
Area of two rectangles=2×height×length=2×8×35=560 m2
- The total internal surface area is the sum of the curved surface area of the semi-circle and the area of the two rectangular sides:
Total Surface Area=CSA of semi-circle+Area of two rectangles=330+560=890 m2
- The cost of plastering is given as Rs 2.25 per m². Therefore, the total cost is:
Total Cost=Total Surface Area×Cost per m2=890×2.25=2002.50 Rs
The cost of plastering the internal surface of the tunnel (excluding the floor) is Rs 2002.50.
Topper's Solved these Questions
- CYLINDER, CONE AND SPHERE BOOK - ICSECHAPTER - CYLINDER, CONE AND SPHERE EXERCISE - EXERCISE 20 (G)
23 Videos
- CYLINDER, CONE AND SPHERE BOOK - ICSECHAPTER - CYLINDER, CONE AND SPHERE EXERCISE - EXERCISE 20 (E)
12 Videos
- CONSTRUCTIONS (CIRCLES)BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE
39 Videos
- EQUATION OF A LINEBOOK - ICSECHAPTER - EQUATION OF A LINEEXERCISE - EXERCISE 14(E)
68 Videos
Similar Questions
The cross-section of a railway tunnel is a square surmounted by a semi-circle as shown in the figure.
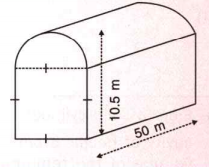
The tunnel is 50 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs 10 per m2.
View SolutionThe cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. The tunnel is 80 m long ,Calculate : its volume
View SolutionThe cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. Calculate: its floor area. The tunnel is 80 m long.
View SolutionThe cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. The tunnel is 80 m long Calculate : the surface area of the tunnel (excluding the floor) .
View SolutionThe cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the following figure, also given that: AM= BN, AB= 7m, CD= 5m. The height of the tunnel is 2.4m. The tunnel is 40m long. Calculate :
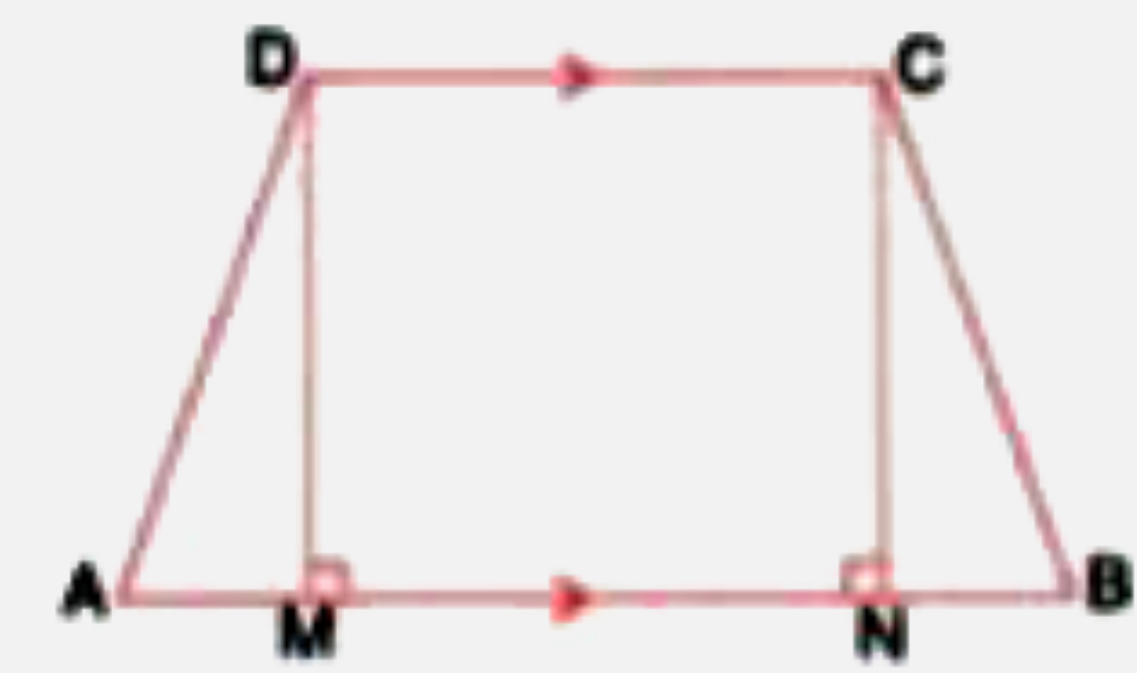
the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of Rs 5 per m2 (sq. metre).
View SolutionA cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of Rs 12.50 per m2.
View SolutionA room is 8 m long and 5 m broad. Find the cost of covering the floor of the room with 80 cm wide carpet at the rate of Rs 225 per metre.
View SolutionFind the cost of painting the border of a rectangular board of length 4 m and breadth 2.5 m at the rate of ₹ 120 per m.
View SolutionA tank is 8m long, 6m broad and 2m high. How much water can it contain?
View SolutionFind the cost of fencing a rectangular park of length 175m and breadth 125m at the rate of Rs. 12 per meter.
View Solution
