The cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. Calculate: its floor area. The tunnel is 80 m long.
The correct Answer is:560m2
To solve the problem, we need to calculate the floor area of the tunnel, which has a cross-section that consists of a square and a semicircle. Here’s the step-by-step solution:
Step 1: Understand the Cross-Section
The cross-section of the tunnel is a square with a side length of 7 m, surmounted by a semicircle. The square's dimensions are as follows:
- Each side of the square = 7 m
Step 2: Calculate the Area of the Square
The area of the square can be calculated using the formula:
Area of the square=side2
Substituting the side length:
Area of the square=72=49m2
Step 3: Calculate the Radius of the Semicircle
The semicircle is placed on top of the square. The diameter of the semicircle is equal to the side of the square. Therefore:
- Diameter of the semicircle = 7 m
- Radius of the semicircle = 72=3.5m
Step 4: Calculate the Area of the Semicircle
The area of a full circle is given by the formula:
Area of the circle=πr2
Since we need the area of a semicircle, we will take half of the area of the circle:
Area of the semicircle=12πr2
Substituting the radius:
Area of the semicircle=12π(3.5)2=12π(12.25)≈19.63495m2
Step 5: Calculate the Total Cross-Sectional Area
Now, we add the area of the square and the area of the semicircle to find the total cross-sectional area:
Total cross-sectional area=Area of the square+Area of the semicircle
Total cross-sectional area=49+19.63495≈68.63495m2
Step 6: Calculate the Floor Area of the Tunnel
The floor area of the tunnel can be calculated by multiplying the total cross-sectional area by the length of the tunnel:
Floor area=Total cross-sectional area×Length of the tunnel
Given that the length of the tunnel is 80 m:
Floor area=68.63495×80≈5490.796m2
Final Answer
The floor area of the tunnel is approximately 5490.80m2.
---
The cross-section of the tunnel is a square with a side length of 7 m, surmounted by a semicircle. The square's dimensions are as follows:
- Each side of the square = 7 m
The area of the square can be calculated using the formula:
Area of the square=side2
Substituting the side length:
Area of the square=72=49m2
The semicircle is placed on top of the square. The diameter of the semicircle is equal to the side of the square. Therefore:
- Diameter of the semicircle = 7 m
- Radius of the semicircle = 72=3.5m
The area of a full circle is given by the formula:
Area of the circle=πr2
Since we need the area of a semicircle, we will take half of the area of the circle:
Area of the semicircle=12πr2
Substituting the radius:
Area of the semicircle=12π(3.5)2=12π(12.25)≈19.63495m2
Now, we add the area of the square and the area of the semicircle to find the total cross-sectional area:
Total cross-sectional area=Area of the square+Area of the semicircle
Total cross-sectional area=49+19.63495≈68.63495m2
The floor area of the tunnel can be calculated by multiplying the total cross-sectional area by the length of the tunnel:
Floor area=Total cross-sectional area×Length of the tunnel
Given that the length of the tunnel is 80 m:
Floor area=68.63495×80≈5490.796m2
The floor area of the tunnel is approximately 5490.80m2.
Topper's Solved these Questions
Similar Questions
The cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. The tunnel is 80 m long Calculate : the surface area of the tunnel (excluding the floor) .
View SolutionThe cross-section of a tunnel is a square of side 7 m surmounted by a semicircle. The tunnel is 80 m long ,Calculate : its volume
View SolutionThe cross-section of a railway tunnel is a square surmounted by a semi-circle as shown in the figure.
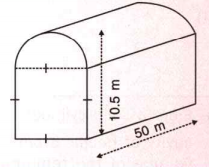
The tunnel is 50 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs 10 per m2.
View SolutionThe cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle . The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of Rs 2.25 per m2
View SolutionFind the area of a square of side 8 m.
View SolutionFind the area of a square of side 14m.
View SolutionFind the area of a square plot of side 8 m.
View SolutionA plot has the shape of a square. Its one side is 24 m long.
Calculate its perimeter.
View SolutionFig. 15.87, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB=90o , calculate: (i) the height of the tunnel (ii) the perimeter of the cross-section (iii) the area of the cross-section.
View SolutionThe cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the following figure, also given that: AM= BN, AB= 7m, CD= 5m. The height of the tunnel is 2.4m. The tunnel is 40m long. Calculate :
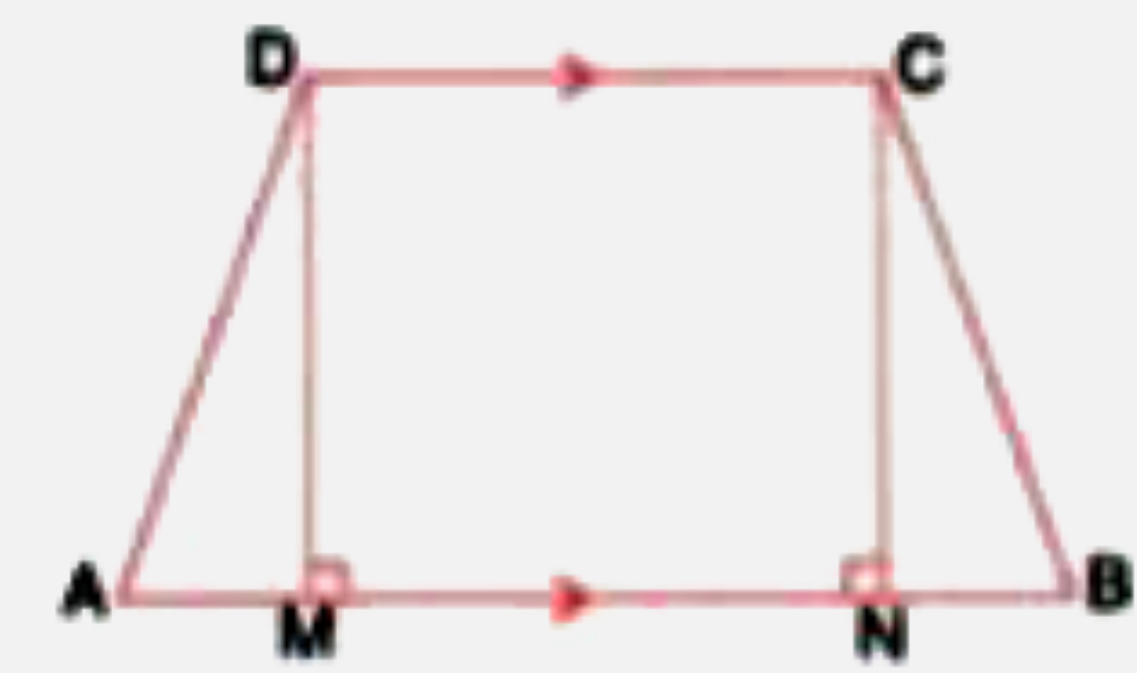
the cost of paying the floor at the rate of Rs 18 per m2.
View Solution
