In a school, the bell for the middle school rings every 30 minutes and the bell for the senior school rings every 40 minutes. The two bells start to ring together at 8.00 a.m. At what time will they ring together again?
The correct Answer is:10.00 a.m
To solve the problem step by step, we need to find the time when both bells will ring together again after starting at 8:00 a.m.
Step 1: Identify the ringing intervals
- The middle school bell rings every 30 minutes.
- The senior school bell rings every 40 minutes.
Step 2: Find the Least Common Multiple (LCM)
To find out when both bells will ring together again, we need to calculate the LCM of 30 and 40.
Step 2.1: Prime Factorization
- 30 can be factored into prime numbers:
- 30=2×3×5
- 40 can be factored into prime numbers:
- 40=23×5
Step 2.2: Determine the LCM
To find the LCM, we take the highest power of each prime number that appears in the factorizations:
- For 2: the highest power is 23 (from 40)
- For 3: the highest power is 31 (from 30)
- For 5: the highest power is 51 (common in both)
Now, we multiply these together:
LCM=23×31×51=8×3×5
Calculating this step by step:
- 8×3=24
- 24×5=120
So, the LCM of 30 and 40 is 120 minutes.
Step 3: Convert LCM to hours and minutes
120 minutes is equivalent to:
120÷60=2 hours
Step 4: Calculate the time when both bells will ring together again
Since both bells start ringing together at 8:00 a.m., we add 2 hours to this time:
8:00 a.m.+2 hours=10:00 a.m.
Final Answer
The two bells will ring together again at 10:00 a.m.
---
- The middle school bell rings every 30 minutes.
- The senior school bell rings every 40 minutes.
To find out when both bells will ring together again, we need to calculate the LCM of 30 and 40.
- 30 can be factored into prime numbers:
- 30=2×3×5
- 40 can be factored into prime numbers:
- 40=23×5
To find the LCM, we take the highest power of each prime number that appears in the factorizations:
- For 2: the highest power is 23 (from 40)
- For 3: the highest power is 31 (from 30)
- For 5: the highest power is 51 (common in both)
LCM=23×31×51=8×3×5
- 8×3=24
- 24×5=120
120 minutes is equivalent to:
120÷60=2 hours
Since both bells start ringing together at 8:00 a.m., we add 2 hours to this time:
8:00 a.m.+2 hours=10:00 a.m.
The two bells will ring together again at 10:00 a.m.
Similar Questions
Three bells ring at an interval of 4, 7 and 12 seconds. They start to ring together at 7.00 a.m. When will they ring together again ?
View SolutionThree bells toll every 6 minutes, 8 minutes and 12 minutes respectively. If they all start tolling at 8.00 a.m. at what time will they toll together again?
View Solution
Knowledge Check
Tours for Qutab Minar, Red Fort and India Gate start from a tourist agency at 10:00a.m. Tours for Qutab Minar leave every 10 minutes, tours for Red Fort leave every 15 minutes and tours for India Gate leave every 30 minutes. At what time will the three tours leave from the agency at the same time again?
A09:30 a.mB11:30 a.mC10:30 a.mD10:45 a.mGecilia leaves home for school on her bike at 9:05 AM, riding at an average speed of 10 miles per hour. Fifteen minutes later, her mother realizes that Cecilia forgot to take her lunch. Cecilia's mother immediately gets into her car and drives after Cecilia at an average speed of 25 miles per hour. At what time will Cecilia mom catch up to her?
A9:15AB9:20AC9:26AD9:30A
Three bells ring at intervals of 4,7and14 minutes. All three range at 6 am. When will they ring together again ?
View SolutionThree bells are ringing continuously at intervals of 30, 36 and 45 minutes respectively. At what time will they ring together again if they ring simultaneously at 8 a.m. ?
View SolutionIn a high -rise building with 84 floors, one delivery boy delivers at every 6th floor and the other at every 8th floor. If the two start delivering together from the entrance of the building, at which floors will they meet again?
View SolutionFour bells toll at intervals of 4, 7, 12 and 84 seconds. The bells toll together at 5 O’clock. When will they again toll together? How many times will they do it in 28 minutes?
View SolutionIn each of the following items, sentence A is complete, while sentence B is not. Complete sentence B, making it as similar as possible to sentence A. Write sentence B in each case.
Example : (0) (A) As soon as the bell rings, the children run out to play.
(B) No sooner..........
Answer : (0) No sooner does the bell ring than the children run out to play.
(A) The doctor said to him, “Drink at least three litres of water every day."
(B) The doctor advised .........
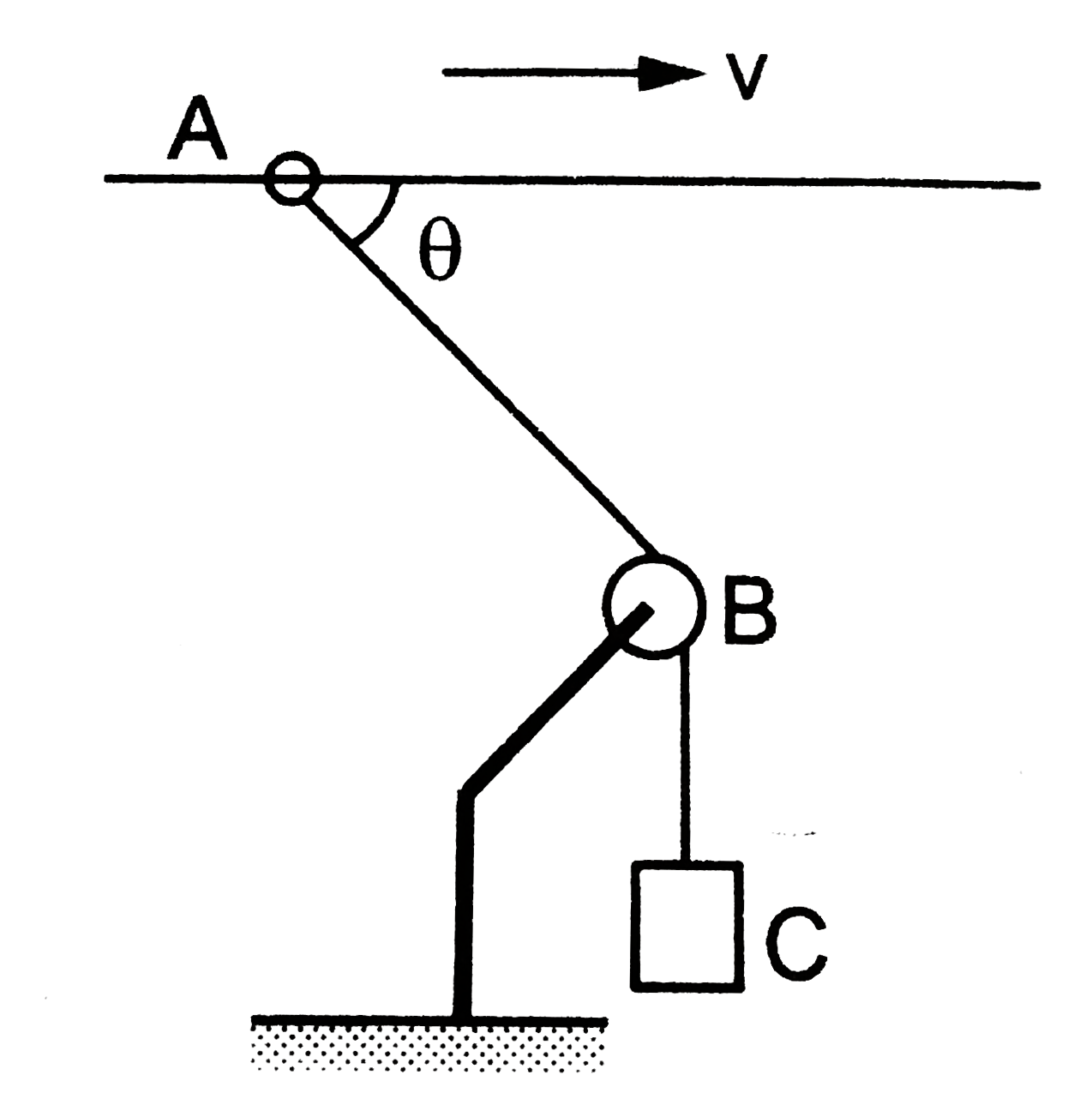
View SolutionA smooth ring A of mass m can slide on a fixed horizontal rod. A string tied to the ring passes over a fixed pulley B and carries a block C of mass M(=2m) as shown in figure. At an instant the string between the ring and the pulley makes an angle θ with the rod. a. Show that, if the ring slides with a speed v, the block descends with speed vcosθ, b. With what acceleration will the ring starts moving if the system is released from rest with θ=300
View Solution