Name a median and an altitude in the figure. Given below if point E is the mid-points of side AC.
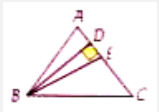
The correct Answer is:Median : BE , Altitude : BD
Step by step video & image solution for Name a median and an altitude in the figure. Given below if point E is the mid-points of side AC. by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Similar Questions
In Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
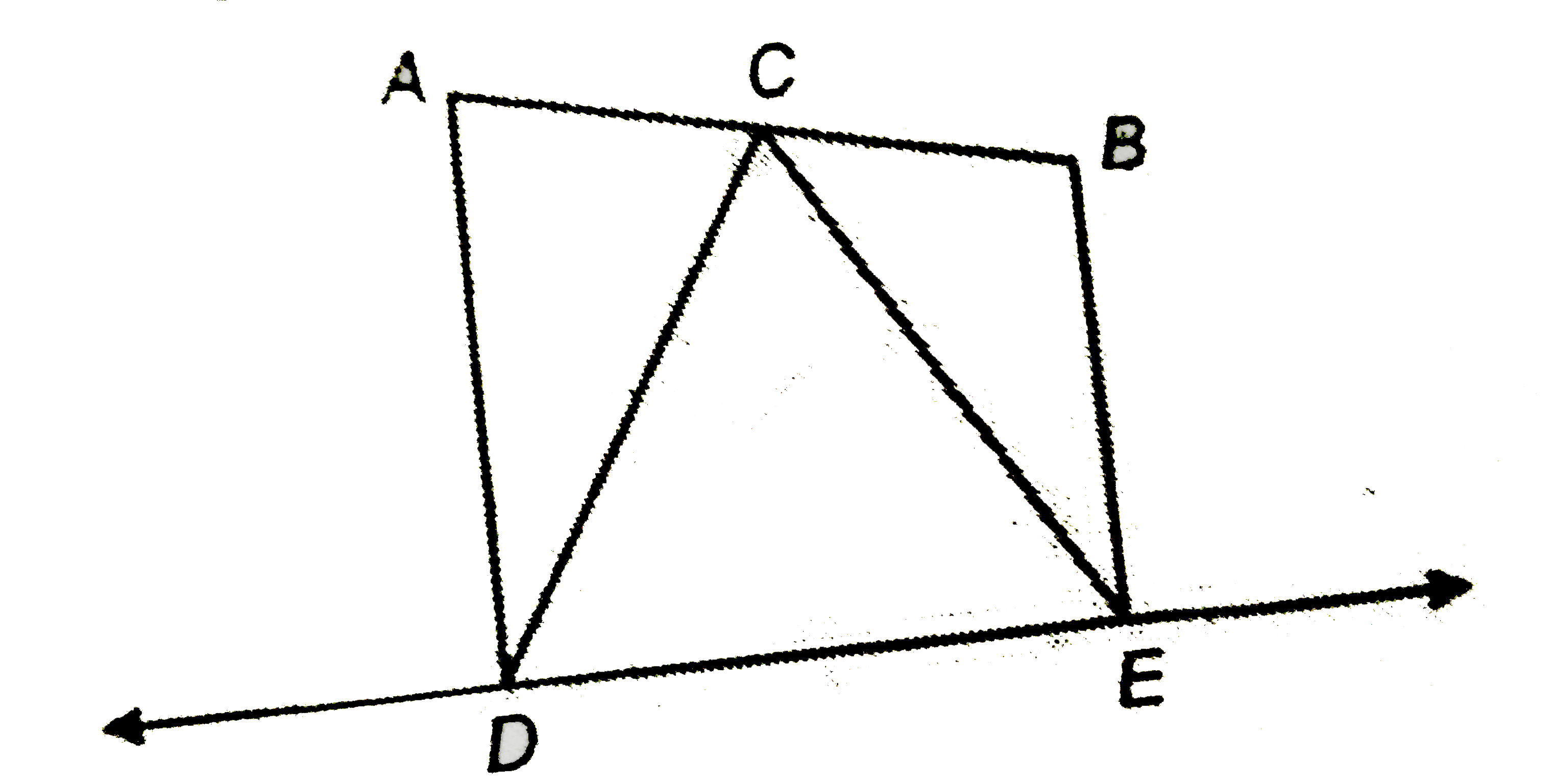
View SolutionIn the adjoining figure, two points A and B lie on the same side of a line 'l'. C is the mid-point of AB. If AD ⊥landBE⊥l, then prove that CD = CE.
View SolutionIn the figure, given below, 2AD=AB,P is the mid-point of AB, Q is the mid-point of DR and PR∣∣BS. Prove that :
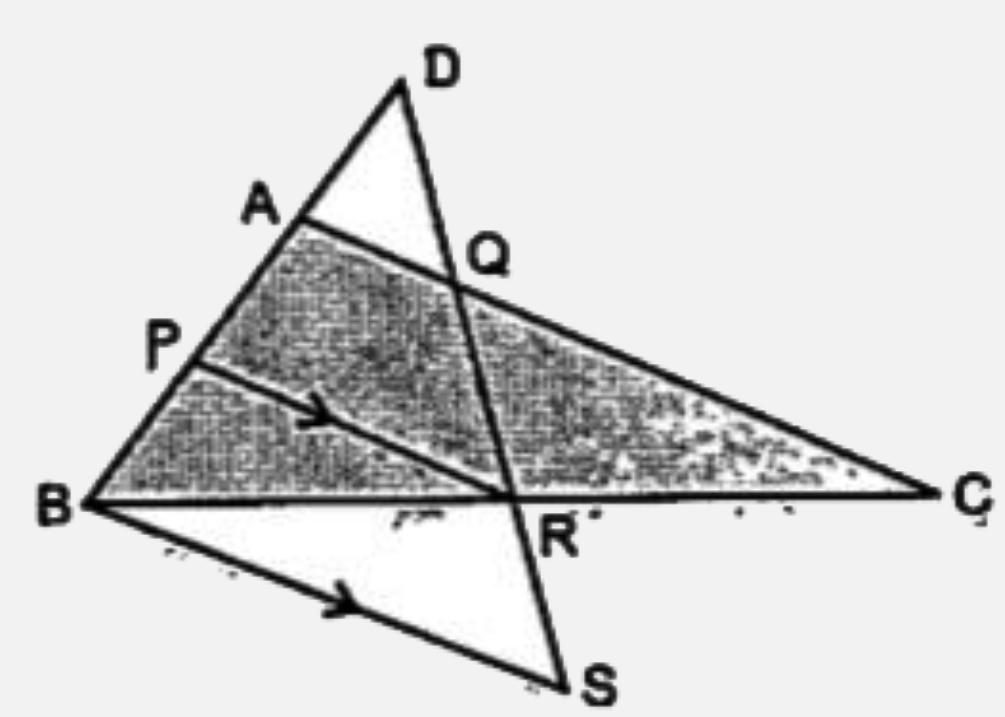
DS=3RS
View SolutionIn the figure, given below, 2AD=AB,P is the mid-point of AB, Q is the mid-point of DR and PR∣∣BS. Prove that :

AQ∣∣BS
View SolutionD is the mid-point of side AB of the triangle ABC.E is the mid-point of CD and F is the mid-point of AE. Prove that 8× area of (ΔAFD)= area of ΔABC
View SolutionIn Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
View SolutionIf in a triangle ABC, the altitude AM be the bisector of ∠BAD, where D is the mid point of side BC, then prove that (b2−c2)=a22.
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionIf in a triangle ABC, the altitude AM be the bisector of ∠BAD,whereD is the mid point of side BC , then prove that (b2−c2)=a2/2.
View SolutionThe diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
View Solution
