If in a triangle ABC, the altitude AM be the bisector of ∠BAD, where D is the mid point of side BC, then prove that (b2−c2)=a22.
Step by step video & image solution for If in a triangle ABC, the altitude AM be the bisector of /_BAD, where D is the mid point of side BC, then prove that (b^2-c^2)= (a^2)/(2). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
If in a triangle ABC, the altitude AM be the bisector of ∠BAD,whereD is the mid point of side BC , then prove that (b2−c2)=a2/2.
View SolutionIn any triangle ABC, prove that AB2+AC2=2(AD2+BD2) , where D is the midpoint of BC.
View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionIn the given figure, triangle ABC is a right triangle with ∠B=90∘andD is mid-point of side BC. Prove that :
AC2=AD2+3CD2

View SolutionIn a triangle ABC, AC>AB , D is the mid-point of BC and AE⊥BC . Prove that: (i) AB2=AD2−BC⋅DE+14BC2
View SolutionIn right-angled triangle ABC in which ∠C=90∘ , if D is the mid-point of BC , prove that AB2=4 AD2−3 AC2 .
View SolutionIn a △ ABC,AB=2,BC=4,CA=3. If D is the mid-point of BC, then the correct statement(s) is/are
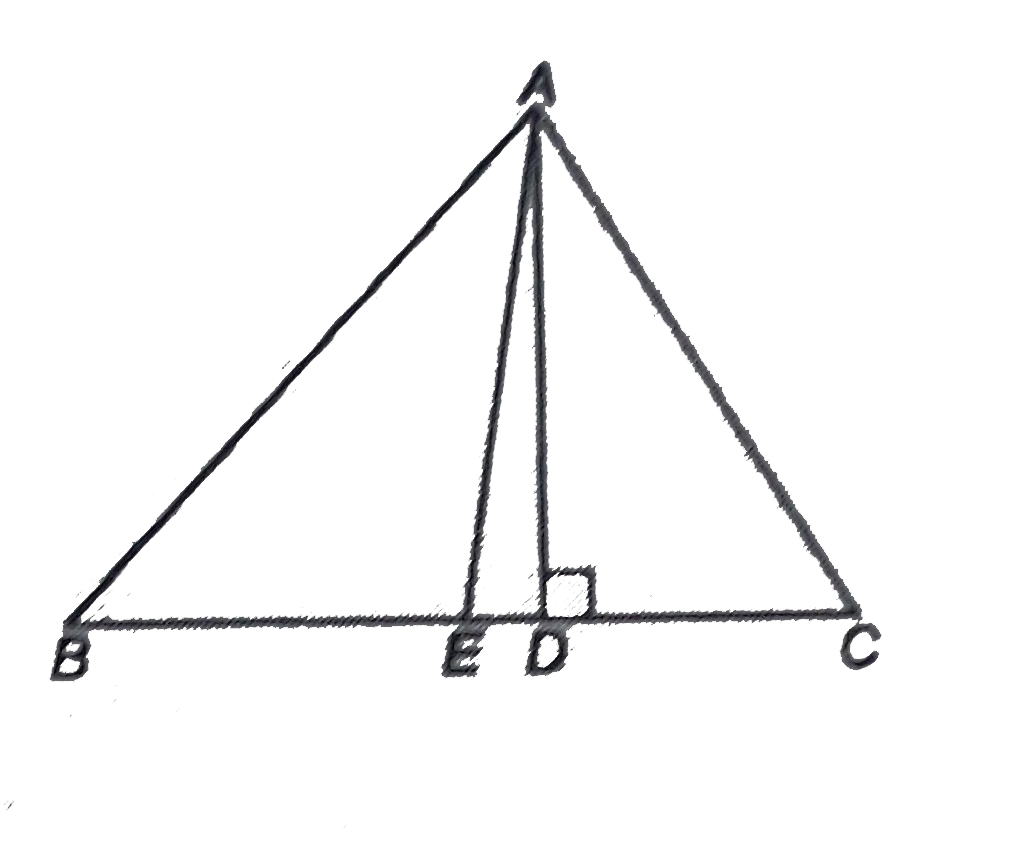
View SolutionThe given figure shows a triangle ABC, in which AB>AC. E is the mid-point of BC and AD is perpendicular to BC. Prove that AB2−AC2=2BC×ED.
View SolutionIn triangle ABC, the line joining the circumcenter and incenter is parallel to side BC, then cosA+cosC is equal to −1 (b) 1 (c) −2 (d) 2
View SolutionD is the mid-point of side BC of △ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(△BOE)=18ar(△ABC).
View Solution
