Can an acute-angled triangled be a. and equilateral, b. an isosceles, and c. a scalene triangle ?
The correct Answer is:(a) Yes
(b) Yes
(c) Yes
To determine whether an acute-angled triangle can be equilateral, isosceles, or scalene, let's analyze each type of triangle step by step.
Step 1: Understanding Acute-Angled Triangle
An acute-angled triangle is defined as a triangle where all three angles are less than 90 degrees.
Step 2: Equilateral Triangle
- Definition: An equilateral triangle has all three sides of equal length and all three angles equal.
- Angles: Since the sum of angles in any triangle is 180 degrees, if all angles are equal in an equilateral triangle, each angle must be:
Angle=1803=60 degrees
- Conclusion: Since 60 degrees is less than 90 degrees, an equilateral triangle is indeed an acute-angled triangle.
Step 3: Isosceles Triangle
- Definition: An isosceles triangle has at least two sides of equal length, which means at least two angles are equal.
- Assumption: Let’s assume the two equal angles are A and B.
- Angle Sum Property: According to the angle sum property:
A+B+C=180 degrees
Since A=B, we can write:
2A+C=180 degrees
- Condition for Acute Angles: If A<90 degrees, then:
2A<180 degrees
This implies:
C=180−2A
Since A is less than 90 degrees, C will also be less than 90 degrees for many values of A (for example, if A=60 degrees, then C=60 degrees).
- Conclusion: Therefore, an isosceles triangle can also be an acute-angled triangle.
Step 4: Scalene Triangle
- Definition: A scalene triangle has all sides of different lengths, which means all angles are different.
- Angle Sum Property: Again, using the angle sum property:
A+B+C=180 degrees
- Example: Let’s take an example where A=40 degrees, B=60 degrees, and C=80 degrees.
- All angles are less than 90 degrees.
- Conclusion: Hence, a scalene triangle can also be an acute-angled triangle.
Final Conclusion
An acute-angled triangle can indeed be:
- a) An equilateral triangle
- b) An isosceles triangle
- c) A scalene triangle
An acute-angled triangle is defined as a triangle where all three angles are less than 90 degrees.
- Definition: An equilateral triangle has all three sides of equal length and all three angles equal.
- Angles: Since the sum of angles in any triangle is 180 degrees, if all angles are equal in an equilateral triangle, each angle must be:
Angle=1803=60 degrees
- Conclusion: Since 60 degrees is less than 90 degrees, an equilateral triangle is indeed an acute-angled triangle.
- Definition: An isosceles triangle has at least two sides of equal length, which means at least two angles are equal.
- Assumption: Let’s assume the two equal angles are A and B.
- Angle Sum Property: According to the angle sum property:
A+B+C=180 degrees
Since A=B, we can write:
2A+C=180 degrees
- Condition for Acute Angles: If A<90 degrees, then:
2A<180 degrees
This implies:
C=180−2A
Since A is less than 90 degrees, C will also be less than 90 degrees for many values of A (for example, if A=60 degrees, then C=60 degrees).
- Conclusion: Therefore, an isosceles triangle can also be an acute-angled triangle.
- Definition: A scalene triangle has all sides of different lengths, which means all angles are different.
- Angle Sum Property: Again, using the angle sum property:
A+B+C=180 degrees
- Example: Let’s take an example where A=40 degrees, B=60 degrees, and C=80 degrees.
- All angles are less than 90 degrees.
- Conclusion: Hence, a scalene triangle can also be an acute-angled triangle.
An acute-angled triangle can indeed be:
- a) An equilateral triangle
- b) An isosceles triangle
- c) A scalene triangle
Topper's Solved these Questions
- THE TRIANGLE AND ITS PROPERTIESBook:ICSEChapter:THE TRIANGLE AND ITS PROPERTIESExercise:EXERCISE 12.3
Explore 12 Videos
- THE TRIANGLE AND ITS PROPERTIESBook:ICSEChapter:THE TRIANGLE AND ITS PROPERTIESExercise:CHALLENGE
Explore 1 Video
- THE TRIANGLE AND ITS PROPERTIESBook:ICSEChapter:THE TRIANGLE AND ITS PROPERTIESExercise:EXERCISE 12.1
Explore 7 Videos
- SYMMETRYBook:ICSEChapter:SYMMETRYExercise:Exercise 19B
Explore 13 Videos
- UNITARY METHODBook:ICSEChapter:UNITARY METHODExercise:EXERCISE
Explore 16 Videos
Similar Questions
Can an equilateral triangle be a, an acute-,b. a right-, and c. an obtuse-angled triangle ? What about isosceles and scalene triangles ?
View SolutionIn an acute-angled triangle ABC, tanA+tanB+tanC
View SolutionIf a vertex, the circumcenter, and the centroid of a triangle are (0, 0), (3,4), and (6, 8), respectively, then the triangle must be (a) a right-angled triangle (b) an equilateral triangle (c) an isosceles triangle (d) a right-angled isosceles triangle
View SolutionIf →xand→y are two non-collinear vectors and a, b, and c represent the sides of a ABC satisfying (a−b)→x+(b−c)→y+(c−a)(→x×→y)=0, then ABC is (where →×x→y is perpendicular to the plane of xandy ) a. an acute-angled triangle b. an obtuse-angled triangle c. a right-angled triangle d. a scalene triangle
View SolutionA triangle whose two sides are equal is called (a) an acute triangle (b) a scalene triangle (c) an isosceles triangle (d) an equilateral triangle
View SolutionIf →xand→y are two non-collinear vectors and ABC isa triangle with side lengths a,b,andc satisfying (20a−15b)→x+(15b−12c)→y+(12c−20a)(→x×→y)=0, then triangle ABC is a. an acute-angled triangle b. an obtuse-angled triangle c. a right-angled triangle d. an isosceles triangle
View SolutionA triangle whose two sides are equal is known as
View SolutionIdentify the following triangles as equilateral, isosceles, scalene, acute-angled, right-angled, and obtuse-angled triangles.
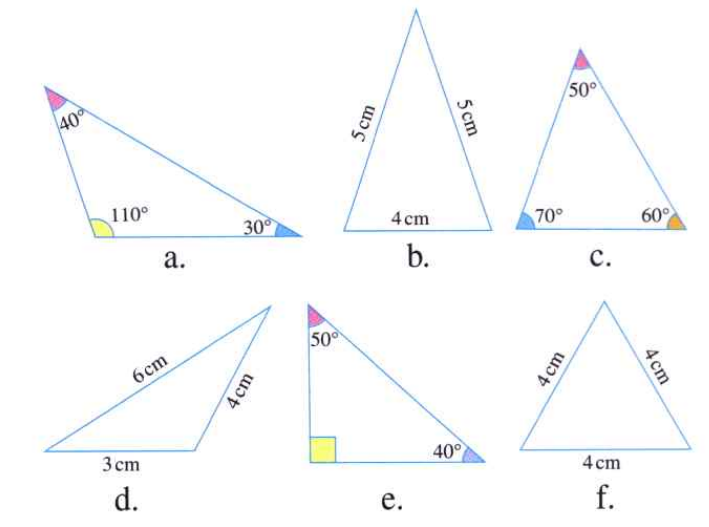
View SolutionIn a triangle ABC a:b:c=√3 :1 : 1, then the triangle is- right angled triangle (b) abtuse angled triangle acute angled triangle, which is not isosceles Equilateral triangle
View Solution- If log(5ca),log(3b5c)and log(a3b)are in AP, where a, b, c are in GP, then a, b, c are the lengths ofsides of(A) an isosceles triangle(B) an equilateral triangle(D) none of these(C) a scalene triangle
View Solution
