The perpendicular from P and QR in the triangle jPQR meets QR at S. Alsl, T is a point on SR sch that QS =3cm,ST=4cm,andT=8cm. Find the ratio of the areas of the triangles PQS , PST and PTR.
The correct Answer is:7:12
To find the ratio of the areas of triangles PQS, PST, and PTR, we can follow these steps:
Step 1: Understand the Problem
We have triangle PQR with a perpendicular from point P to line QR meeting at point S. Point T is on segment SR. We know the lengths of segments QS, ST, and TR.
Step 2: Identify Given Values
- QS = 3 cm
- ST = 4 cm
- TR = 8 cm
Step 3: Calculate Length of SR
To find the length of segment SR, we can add the lengths of QS and ST:
SR=QS+ST=3 cm+4 cm=7 cm
Step 4: Determine the Length of QR
The total length of QR can be calculated by adding the lengths of QS, ST, and TR:
QR=QS+ST+TR=3 cm+4 cm+8 cm=15 cm
Step 5: Use the Area Formula
The area of a triangle is given by the formula:
Area=12×base×height
Here, the height (PS) is common for all triangles.
Step 6: Write the Area Expressions
- Area of triangle PQS:
AreaPQS=12×QS×PS=12×3×PS
- Area of triangle PST:
AreaPST=12×ST×PS=12×4×PS
- Area of triangle PTR:
AreaPTR=12×TR×PS=12×8×PS
Step 7: Set Up the Ratios
Now we can set up the ratios of the areas:
AreaPQS:AreaPST:AreaPTR=(3×PS):(4×PS):(8×PS)
Step 8: Simplify the Ratios
Since PS is common in all three areas, it cancels out:
3:4:8
Final Answer
The ratio of the areas of triangles PQS, PST, and PTR is:
Ratio=3:4:8
We have triangle PQR with a perpendicular from point P to line QR meeting at point S. Point T is on segment SR. We know the lengths of segments QS, ST, and TR.
- QS = 3 cm
- ST = 4 cm
- TR = 8 cm
To find the length of segment SR, we can add the lengths of QS and ST:
SR=QS+ST=3 cm+4 cm=7 cm
The total length of QR can be calculated by adding the lengths of QS, ST, and TR:
QR=QS+ST+TR=3 cm+4 cm+8 cm=15 cm
The area of a triangle is given by the formula:
Area=12×base×height
Here, the height (PS) is common for all triangles.
- Area of triangle PQS:
AreaPQS=12×QS×PS=12×3×PS
- Area of triangle PST:
AreaPST=12×ST×PS=12×4×PS
- Area of triangle PTR:
AreaPTR=12×TR×PS=12×8×PS
Now we can set up the ratios of the areas:
AreaPQS:AreaPST:AreaPTR=(3×PS):(4×PS):(8×PS)
Since PS is common in all three areas, it cancels out:
3:4:8
The ratio of the areas of triangles PQS, PST, and PTR is:
Ratio=3:4:8
Topper's Solved these Questions
- BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - EXERCISE 17.316videos
PERIMETER AND AREA
- BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - REVISION EXERCISE24videos
PERIMETER AND AREA
- BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - EXERCISE 17.115videos
PERIMETER AND AREA
- BOOK - ICSECHAPTER - PERCENTAGE, PROFIT AND LOSSEXERCISE - REVISION EXERCISE26videos
PERCENTAGE, PROFIT AND LOSS
- BOOK - ICSECHAPTER - PROBABILITYEXERCISE - TRY THIS14videos
PROBABILITY
Similar Questions
In ΔABC, the perependicular from A BC meets BC at D such that BD=7cmandDC=12cm.Find the ratio of the areas of the triangles ABD and ADC.
View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View SolutionIn ΔPQR,PR=8cm,QR=4cmandPL=5cm (Fig 11.22). Find: (i) the area of the ΔPQR (ii) QM
View SolutionA triangle ABC is such that AD is perpendicular to BC and E is a point on DC. Also. Given that BD=2cm,DE=4cm,andEC=8cm. Find the ratio of the areas of ΔABC , ΔADEandΔAEC.
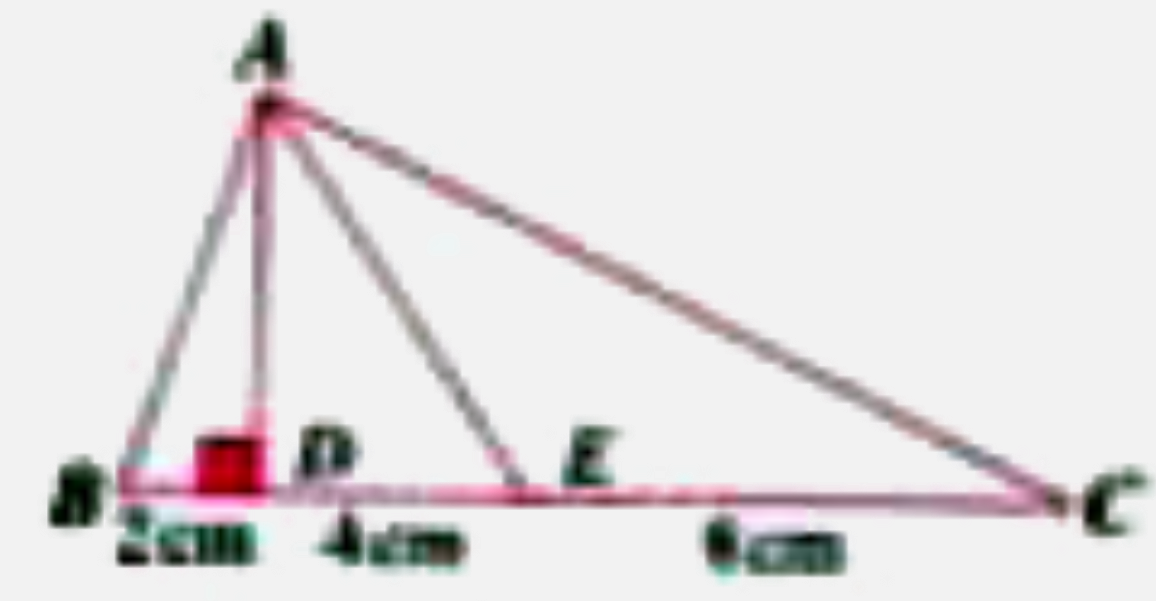 View Solution
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Find the lengths of QR and PS.View SolutionConstruct a triangle PQR given that PQ = 5 cm, QR = 4 cm and PR = 3 cm . Measure ∠PRQ and name the triangle.
View SolutionA circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths QM, RN and PL.
View SolutionA circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths QM, RN and PL.
View SolutionSides of a triangle are in the ratio 3:4:5 and its area is 54cm2 Find the sides of the triangle.
View SolutionIn the given figure, ∠B=∠E,∠ACD=∠BCE,AB=10.4 cm and DE=7.8cm. Find the ratio between areas of the ΔABCandΔDEC.
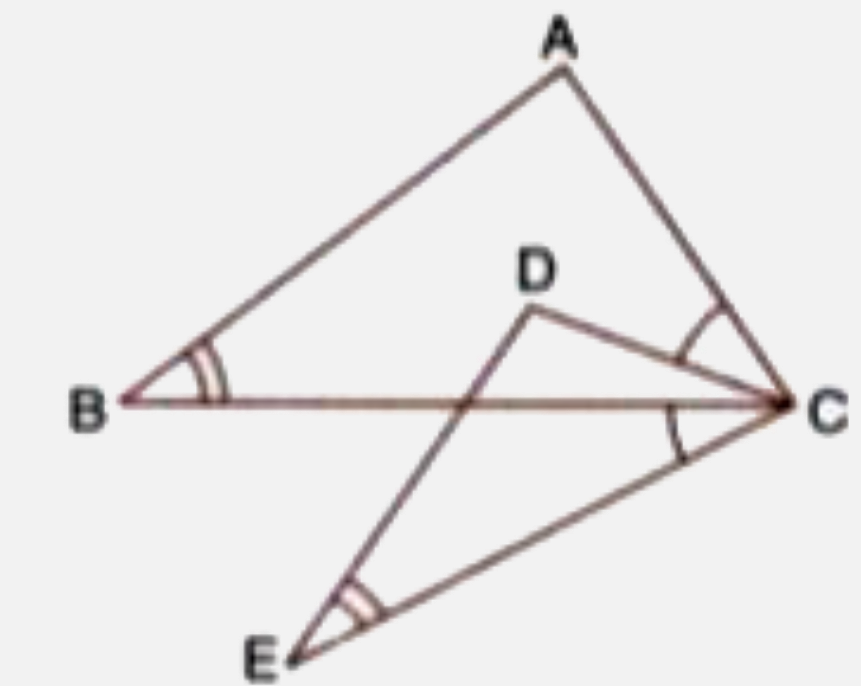 View Solution
View Solution

