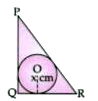
A circle is inscribed in a triangle PQR with PQ = 10 cm, QR = 8 cm and PR = 12 cm. Find the lengths QM, RN and PL.
To solve the problem of finding the lengths QM, RN, and PL in triangle PQR with sides PQ = 10 cm, QR = 8 cm, and PR = 12 cm, we can follow these steps:
Step 1: Understand the Problem
We have a triangle PQR with an inscribed circle. The points where the circle touches the sides of the triangle are denoted as M, N, and L. We need to find the lengths of QM, RN, and PL.
Step 2: Set Up the Variables
Let:
- QM = x
- RN = y
- PL = z
From the properties of tangents drawn from an external point to a circle, we know:
- QM = x
- MR = y
- PL = z
- PN = z
- NR = y
- LQ = x
Step 3: Write the Equations
Using the sides of the triangle, we can write the following equations based on the segments:
1. QR = QM + MR → 8 = x + y (Equation 1)
2. PQ = PL + LQ → 10 = z + x (Equation 2)
3. PR = PN + NR → 12 = z + y (Equation 3)
Step 4: Solve the Equations
Now we have three equations:
1. x+y=8 (Equation 1)
2. z+x=10 (Equation 2)
3. z+y=12 (Equation 3)
Step 4.1: Express y in terms of x
From Equation 1:
y=8−x
Step 4.2: Substitute y in Equation 3
Substituting y in Equation 3:
z+(8−x)=12
z+8−x=12
z−x=4
z=x+4 (Equation 4)
Step 4.3: Substitute z in Equation 2
Now substituting z in Equation 2:
(x+4)+x=10
2x+4=10
2x=6
x=3
Step 4.4: Find y and z
Now, substituting x back to find y and z:
- From Equation 1:
y=8−x=8−3=5
- From Equation 4:
z=x+4=3+4=7
Final Results
Thus, we have:
- QM = x = 3 cm
- RN = y = 5 cm
- PL = z = 7 cm
Conclusion
The lengths are:
- QM = 3 cm
- RN = 5 cm
- PL = 7 cm
We have a triangle PQR with an inscribed circle. The points where the circle touches the sides of the triangle are denoted as M, N, and L. We need to find the lengths of QM, RN, and PL.
Let:
- QM = x
- RN = y
- PL = z
- QM = x
- MR = y
- PL = z
- PN = z
- NR = y
- LQ = x
Using the sides of the triangle, we can write the following equations based on the segments:
1. QR = QM + MR → 8 = x + y (Equation 1)
2. PQ = PL + LQ → 10 = z + x (Equation 2)
3. PR = PN + NR → 12 = z + y (Equation 3)
Now we have three equations:
1. x+y=8 (Equation 1)
2. z+x=10 (Equation 2)
3. z+y=12 (Equation 3)
From Equation 1:
y=8−x
Substituting y in Equation 3:
z+(8−x)=12
z+8−x=12
z−x=4
z=x+4 (Equation 4)
Now substituting z in Equation 2:
(x+4)+x=10
2x+4=10
2x=6
x=3
Now, substituting x back to find y and z:
- From Equation 1:
y=8−x=8−3=5
- From Equation 4:
z=x+4=3+4=7
Thus, we have:
- QM = x = 3 cm
- RN = y = 5 cm
- PL = z = 7 cm
The lengths are:
- QM = 3 cm
- RN = 5 cm
- PL = 7 cm
Topper's Solved these Questions
Similar Questions
PQRS is a parallelogram with PQ=15cm,ST=10cm,andQV=12cm. Find PS.
View SolutionConstruct a triangle PQR with sides PQ = 5 cm, QR = 4 cm, and ∠PQR=100∘.
View SolutionConstruct a triangle PQR in which QR = 6cm, ∠Q=60∘ and PR – PQ = 2cm.
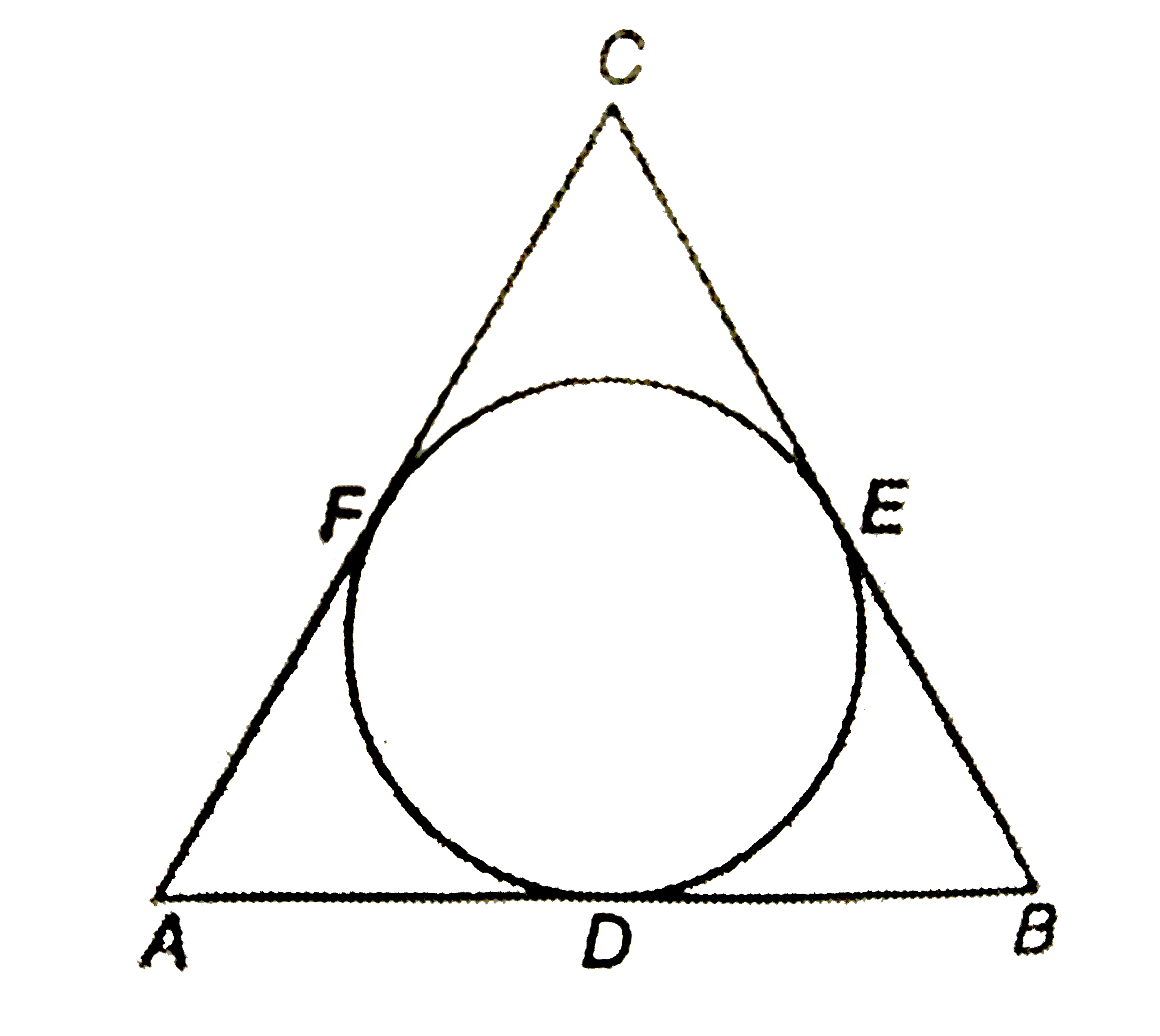
View SolutionA circle is inscribed in a △ABC having sides 8 cm, 10 cm and 12 cm as shown in figure. Find AD, BE and CF.
View SolutionIn triangle PQR, PQ = 24 cm, QR = 7 cm and ∠PQR=90∘. Find the radius of the inscribed circle.
View SolutionConstruct a triangle PQR given that PQ = 5 cm, QR = 4 cm and PR = 3 cm . Measure ∠PRQ and name the triangle.
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Find the lengths of QR and PS.
View SolutionPQR is a triangle right angled at P. If PQ=10cmandPR=24cm, find QR
View SolutionIn ΔPQR, If angleR=angleP, QR=4 cm and PR = 5 cm. Then, the length of PQ is
View SolutionIn the figure: ∠PSQ=90∘,PQ=10cm,QS=6cmand RQ=9cm. Find the value of PR.

View Solution
