A square garden measures 30 m by 30 m. Two flower beds in the shape of a quarter circles are made with two opposite vertices as centres. If the radius of each of the quarter circles is 7 m, find the portion of the garden with grass.
The correct Answer is:823sq.cm
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the area of the square garden.
The area of a square is given by the formula:
Area=side×side
Given that the side of the square garden is 30 m:
Area=30m×30m=900m2
Step 2: Calculate the area of one quarter circle.
The area of a full circle is given by the formula:
Area=πr2
Since we need the area of a quarter circle, we will divide the area of the full circle by 4:
Area of quarter circle=πr24
Given that the radius r is 7 m:
Area of quarter circle=π(7m)24=π×49m24
Step 3: Substitute the value of π.
Using π≈227:
Area of quarter circle=227×494=22×4928=107828=38.5m2
Step 4: Calculate the area of two quarter circles.
Since there are two quarter circles:
Area of two quarter circles=2×Area of one quarter circle=2×38.5m2=77m2
Step 5: Calculate the area of the garden with grass.
To find the area of the garden that remains with grass, subtract the area of the flower beds from the area of the square garden:
Area with grass=Area of square garden−Area of flower beds
Area with grass=900m2−77m2=823m2
Final Answer:
The portion of the garden with grass is 823m2.
---
The area of a square is given by the formula:
Area=side×side
Given that the side of the square garden is 30 m:
Area=30m×30m=900m2
The area of a full circle is given by the formula:
Area=πr2
Since we need the area of a quarter circle, we will divide the area of the full circle by 4:
Area of quarter circle=πr24
Given that the radius r is 7 m:
Area of quarter circle=π(7m)24=π×49m24
Using π≈227:
Area of quarter circle=227×494=22×4928=107828=38.5m2
Since there are two quarter circles:
Area of two quarter circles=2×Area of one quarter circle=2×38.5m2=77m2
To find the area of the garden that remains with grass, subtract the area of the flower beds from the area of the square garden:
Area with grass=Area of square garden−Area of flower beds
Area with grass=900m2−77m2=823m2
The portion of the garden with grass is 823m2.
Topper's Solved these Questions
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - REVISION EXERCISE
24 Videos
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - UNIT PRACTICE PAPER V
10 Videos
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - EXERCISE 17.2
33 Videos
- PERCENTAGE, PROFIT AND LOSSBOOK - ICSECHAPTER - PERCENTAGE, PROFIT AND LOSSEXERCISE - REVISION EXERCISE
26 Videos
- PROBABILITYBOOK - ICSECHAPTER - PROBABILITYEXERCISE - TRY THIS
14 Videos
Similar Questions
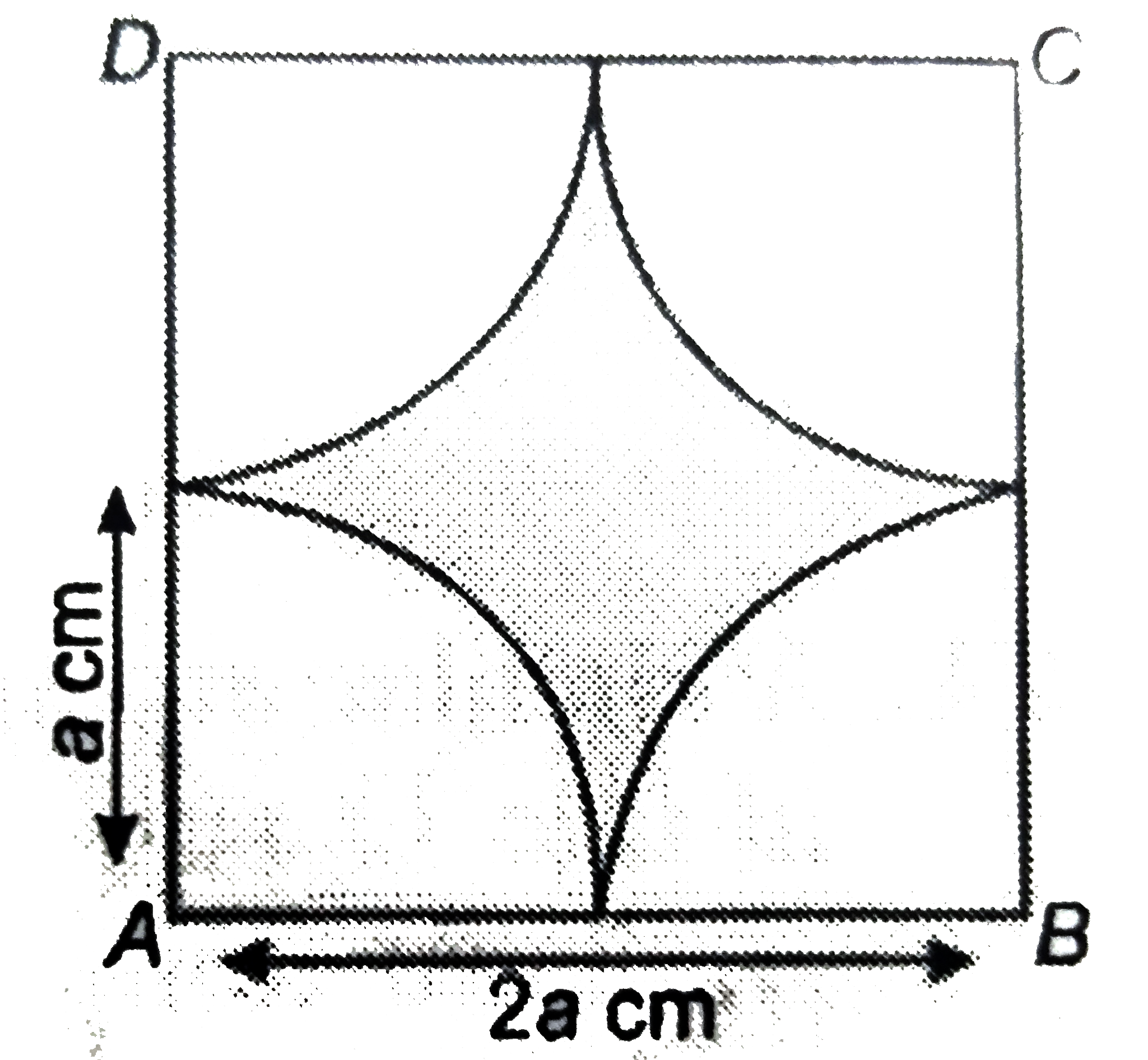
In the square ABCD with side 2acm, four quarter circles are drawn with the vertices as centres and radius acm. Find the area of the shaded portion.
View SolutionA wire of 5024 m length is in the form of a square. It is cut and made a circle. Find the ratio of the area of the square to that of the circle.
View Solution
Knowledge Check
The area of a garden in the shape of a square is 5184 m2 . Find its perimeter .
A=388 m.B=288 m.C=188 m.D=298 m.
The perimeter of a sector a circle of radius 5.7 m is 27.2 m. Find the area of the sector.
View SolutionThe perimeter of a certain sector of a circle of radius 5.7 m is 27.2 m. find the area of the sector
View SolutionMatt has a garden in the shape of a right-angled triangle with one of the acute angles as 30∘ . If the longest side of the triangle is 4 m long, what is the perimeter, in meters , of the garden?
View SolutionThe perimeter of a certain sector of a circle of radius 5.7 m is 27.2 m. Find the area of the sector.
View SolutionA circle field has perimeter 660m. Plot in the shape of a square having its vertices on the circumference is marked in the field. Calculate the area of the square field
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View SolutionTwo chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
View Solution
