In ΔAST, where TP⊥SA, area equals 204 sq. cm. Given that TP=17cmand area of ΔTSP: area of ΔTAP=3:5, find SP and PA.
The correct Answer is:4:25
To solve the problem step by step, we will follow the logic presented in the video transcript.
Step 1: Understand the given information
We have a triangle AST with a perpendicular TP drawn to the base SA. The area of triangle AST is given as 204 sq. cm, and the height TP is 17 cm. The area ratio of triangles TSP and TAP is given as 3:5.
Step 2: Calculate the length of base AS
The area of a triangle can be calculated using the formula:
Area=12×base×height
For triangle AST:
204=12×AS×TP
Substituting the known values:
204=12×AS×17
Multiplying both sides by 2:
408=AS×17
Now, divide both sides by 17 to find AS:
AS=40817=24 cm
Step 3: Express AS in terms of AP and PS
Let:
AS=AP+PS(Equation 1)
Since we found that AS=24 cm, we can write:
AP+PS=24 cm
Step 4: Set up the ratio of areas
The ratio of the areas of triangles TSP and TAP is given as:
Area of TSPArea of TAP=35
Using the area formula for both triangles:
12×TP×PS12×TP×PA=35
The 12×TP cancels out:
PSPA=35(Equation 2)
Step 5: Express PS in terms of PA
From Equation 2, we can express PS in terms of PA:
PS=35PA
Step 6: Substitute PS in Equation 1
Substituting PS in Equation 1:
AP+35PA=24
Let AP=PA−PS:
PA−35PA+35PA=24
This simplifies to:
PA+PS=24
Now substituting PS=35PA:
PA+35PA=24
Combining the terms:
85PA=24
Step 7: Solve for PA
Multiply both sides by 58:
PA=24×58=15 cm
Step 8: Find SP using Equation 1
Now, substitute PA back into Equation 1 to find SP:
AP+PS=24
We know PS=35×15=9 cm:
AP+9=24
Thus:
AP=24−9=15 cm
Final Results
- Length of side PA=15 cm
- Length of side SP=9 cm
We have a triangle AST with a perpendicular TP drawn to the base SA. The area of triangle AST is given as 204 sq. cm, and the height TP is 17 cm. The area ratio of triangles TSP and TAP is given as 3:5.
The area of a triangle can be calculated using the formula:
Area=12×base×height
For triangle AST:
204=12×AS×TP
Substituting the known values:
204=12×AS×17
Multiplying both sides by 2:
408=AS×17
Now, divide both sides by 17 to find AS:
AS=40817=24 cm
Let:
AS=AP+PS(Equation 1)
Since we found that AS=24 cm, we can write:
AP+PS=24 cm
The ratio of the areas of triangles TSP and TAP is given as:
Area of TSPArea of TAP=35
Using the area formula for both triangles:
12×TP×PS12×TP×PA=35
The 12×TP cancels out:
PSPA=35(Equation 2)
From Equation 2, we can express PS in terms of PA:
PS=35PA
Substituting PS in Equation 1:
AP+35PA=24
Let AP=PA−PS:
PA−35PA+35PA=24
This simplifies to:
PA+PS=24
Now substituting PS=35PA:
PA+35PA=24
Combining the terms:
85PA=24
Multiply both sides by 58:
PA=24×58=15 cm
Now, substitute PA back into Equation 1 to find SP:
AP+PS=24
We know PS=35×15=9 cm:
AP+9=24
Thus:
AP=24−9=15 cm
- Length of side PA=15 cm
- Length of side SP=9 cm
Topper's Solved these Questions
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - UNIT PRACTICE PAPER V
10 Videos
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - TRY THIS
41 Videos
- PERIMETER AND AREA BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - EXERCISE 17.3
16 Videos
- PERCENTAGE, PROFIT AND LOSSBOOK - ICSECHAPTER - PERCENTAGE, PROFIT AND LOSSEXERCISE - REVISION EXERCISE
26 Videos
- PROBABILITYBOOK - ICSECHAPTER - PROBABILITYEXERCISE - TRY THIS
14 Videos
Similar Questions
In ΔLMN,NT⊥LM. Area of ΔLMN=72sq.mandNT=9cm. If area of ΔNTL, area of ΔNTM=1:3, find LT and TM.
View SolutionIn ΔPQR.PS⊥QR.PS=11cmand area of ΔPQR=77sq.cmIfareaofDelta PSQ: areaofDelta PSR = 3:4. f∈dQS and SR.
View SolutionIn DetlaABC,AD is perpendicular to BC. If AD = 12 cm, area of ΔADB=90sq.cm. and area of DetlaADB: area De≤taADC=2:3, find BD and DC.

View SolutionThe area of a triangle is 192 sq.cm and its height is 12 cm. Find its base.
View SolutionThe area of a triangle is 315sq.cm. If the base is 18 cm, find its altitude.
View SolutionIn the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
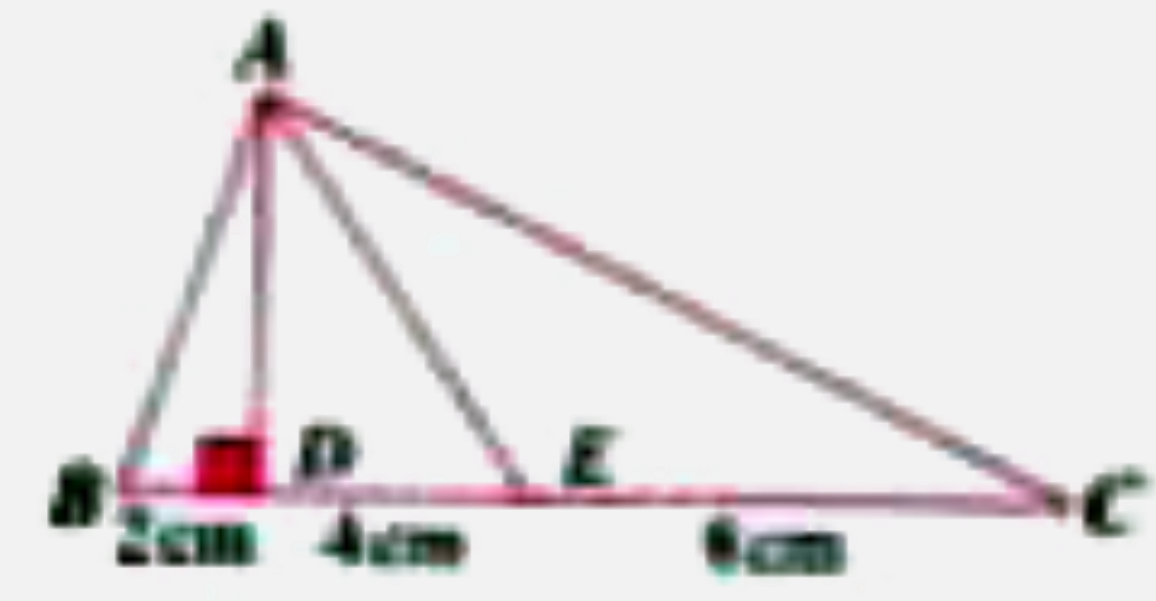
View SolutionA triangle ABC is such that AD is perpendicular to BC and E is a point on DC. Also. Given that BD=2cm,DE=4cm,andEC=8cm. Find the ratio of the areas of ΔABC , ΔADEandΔAEC.
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

area of ΔPQRarea of ΔSPR
View SolutionIn the figure, given alongside, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and area of ΔPOB−120cm2. find the area of ΔQOA.

View SolutionABCD is a parallelogram DP is perpendicular to AB. Given BD=5cm,AP=3cm.and area of ΔADP=6 sq. cm, find the perimeter of ABCD.
View Solution
