The shortest distance that takes direction into account is called displacement.
To determine whether the statement "The shortest distance that takes direction into account is called displacement" is true or false, we can follow these steps:
1. Understand the Definition of Displacement:
- Displacement is defined as the shortest distance between two points in a specific direction. It is a vector quantity, meaning it has both magnitude and direction.
2. Identify Points:
- Let's consider two points, A and B. We can visualize these points on a plane or graph.
3. Consider Different Paths:
- There can be multiple paths to travel from point A to point B. For example, one might take a curved path, a zigzag path, or a straight line.
4. Determine the Shortest Path:
- Among all possible paths from A to B, the straight line connecting A and B represents the shortest distance. This is the direct path.
5. Incorporate Direction:
- Since displacement takes direction into account, the straight line from A to B not only represents the shortest distance but also indicates the direction from A to B.
6. Conclusion:
- Therefore, the statement "The shortest distance that takes direction into account is called displacement" is indeed true.
Final Answer:
The statement is True.
---
- Displacement is defined as the shortest distance between two points in a specific direction. It is a vector quantity, meaning it has both magnitude and direction.
- Let's consider two points, A and B. We can visualize these points on a plane or graph.
- There can be multiple paths to travel from point A to point B. For example, one might take a curved path, a zigzag path, or a straight line.
- Among all possible paths from A to B, the straight line connecting A and B represents the shortest distance. This is the direct path.
- Since displacement takes direction into account, the straight line from A to B not only represents the shortest distance but also indicates the direction from A to B.
- Therefore, the statement "The shortest distance that takes direction into account is called displacement" is indeed true.
The statement is True.
Topper's Solved these Questions
- FORCE AND PRESSURE : MOTION BOOK - ICSECHAPTER - FORCE AND PRESSURE : MOTION EXERCISE - EXERCISES (SECTION I)
15 Videos
- FORCE AND PRESSURE : MOTION BOOK - ICSECHAPTER - FORCE AND PRESSURE : MOTION EXERCISE - EXERCISES (SECTION I) (Write T for True and F for False. Correct the false statements.)
1 Videos
- FORCE AND PRESSURE : MOTION BOOK - ICSECHAPTER - FORCE AND PRESSURE : MOTION EXERCISE - EXERCISES (SECTION II) (Picture Study)
4 Videos
- ENERGYBOOK - ICSECHAPTER - ENERGYEXERCISE - EXERCISE (PICTURE STUDY)
3 Videos
- HEATBOOK - ICSECHAPTER - HEATEXERCISE - EXERCISE (PICTURE)
10 Videos
Similar Questions
Knowledge Check
Respiration in insects Is called direct because
Athe cells exchange O2/CO2 directly with the air in the tubesBthe tissues exchange O2/CO2 directly with coelomic fluidCthe tissues exchange O2/CO2 directly with the air outside thorugh body surfaceDtracheal tubes exchange O2/CO2 directly with the haemocoel which then exchange with tissues.Assertion , No work is done if the displacement is zero
Reason: Work done by the force is defined to be the product of component of the force in the the direction of the displacement and the magnitude of displacement.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true not but reason is not the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.
Respiration in insects Is called direct because
View SolutionMultiple gene inheritance takes into account
View SolutionFill in Blanks:
No work is done when ____takes places at right angles to the direction of applied force. (displacement/acceleration).
View SolutionThe shortest distance between origin and a point on the space curve x=2sint,y=2cost,z=3t is….
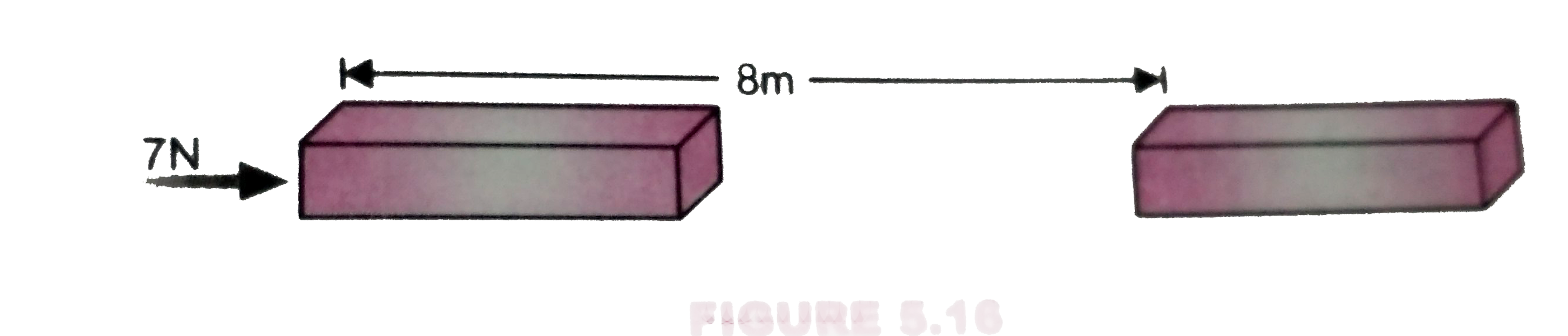
View SolutionA force of 7N acts on an object. The displacement is, say 8m, in the direction of the force, Let us take it that the force acts on the object throughout the displacement. What is the work done in this case ?
View SolutionThe shortest distance between a diagonal of a unit cube and the edge skew to it, is
View Solution
