The shortest distance between a diagonal of a unit cube and the edge skew to it, is
The correct Answer is:A
To find the shortest distance between a diagonal of a unit cube and an edge skew to it, we can follow these steps:
Step 1: Define the points of the cube
Let's define the vertices of the unit cube. The vertices can be represented as:
- O(0,0,0)
- A(1,1,1)
- B(1,0,1)
- C(1,0,0)
- D(0,1,0)
- E(0,0,1)
- F(0,1,1)
- G(1,1,0)
Step 2: Identify the diagonal and the skew edge
The diagonal we will consider is OA which connects points O(0,0,0) and A(1,1,1). The skew edge we will consider is BC which connects points B(1,0,1) and C(1,0,0).
Step 3: Find the midpoint of the diagonal
To find the midpoint D of diagonal OA:
D=(0+12,0+12,0+12)=(12,12,12)
Step 4: Find the midpoint of the skew edge
To find the midpoint E of edge BC:
E=(1+12,0+02,1+02)=(1,0,12)
Step 5: Determine the direction vectors
The direction vector of diagonal OA is:
→d1=A−O=(1,1,1)−(0,0,0)=(1,1,1)
The direction vector of edge BC is:
→d2=C−B=(1,0,0)−(1,0,1)=(0,0,−1)
Step 6: Calculate the shortest distance
The shortest distance D between the two skew lines can be calculated using the formula:
D=|(→d1×→d2)⋅→PQ||→d1×→d2|
Where →PQ is the vector connecting points O and B:
→PQ=B−O=(1,0,1)−(0,0,0)=(1,0,1)
Step 7: Calculate the cross product
First, we calculate the cross product →d1×→d2:
→d1×→d2=∣∣
∣
∣∣^i^j^k11100−1∣∣
∣
∣∣=^i(1⋅(−1)−1⋅0)−^j(1⋅(−1)−1⋅0)+^k(1⋅0−1⋅0)
=−^i+^j+0^k=(−1,1,0)
Step 8: Calculate the magnitude of the cross product
Now, we calculate the magnitude of →d1×→d2:
|→d1×→d2|=√(−1)2+12+02=√1+1=√2
Step 9: Calculate the dot product
Next, we calculate the dot product (→d1×→d2)⋅→PQ:
(−1,1,0)⋅(1,0,1)=−1⋅1+1⋅0+0⋅1=−1
Step 10: Substitute into the distance formula
Now, substitute into the distance formula:
D=|(−1)|√2=1√2=√22
Conclusion
Thus, the shortest distance between the diagonal of the unit cube and the edge skew to it is:
√22
---
Let's define the vertices of the unit cube. The vertices can be represented as:
- O(0,0,0)
- A(1,1,1)
- B(1,0,1)
- C(1,0,0)
- D(0,1,0)
- E(0,0,1)
- F(0,1,1)
- G(1,1,0)
The diagonal we will consider is OA which connects points O(0,0,0) and A(1,1,1). The skew edge we will consider is BC which connects points B(1,0,1) and C(1,0,0).
To find the midpoint D of diagonal OA:
D=(0+12,0+12,0+12)=(12,12,12)
To find the midpoint E of edge BC:
E=(1+12,0+02,1+02)=(1,0,12)
The direction vector of diagonal OA is:
→d1=A−O=(1,1,1)−(0,0,0)=(1,1,1)
The direction vector of edge BC is:
→d2=C−B=(1,0,0)−(1,0,1)=(0,0,−1)
The shortest distance D between the two skew lines can be calculated using the formula:
D=|(→d1×→d2)⋅→PQ||→d1×→d2|
Where →PQ is the vector connecting points O and B:
→PQ=B−O=(1,0,1)−(0,0,0)=(1,0,1)
First, we calculate the cross product →d1×→d2:
→d1×→d2=∣∣
∣
∣∣^i^j^k11100−1∣∣
∣
∣∣=^i(1⋅(−1)−1⋅0)−^j(1⋅(−1)−1⋅0)+^k(1⋅0−1⋅0)
=−^i+^j+0^k=(−1,1,0)
Now, we calculate the magnitude of →d1×→d2:
|→d1×→d2|=√(−1)2+12+02=√1+1=√2
Next, we calculate the dot product (→d1×→d2)⋅→PQ:
(−1,1,0)⋅(1,0,1)=−1⋅1+1⋅0+0⋅1=−1
Now, substitute into the distance formula:
D=|(−1)|√2=1√2=√22
Thus, the shortest distance between the diagonal of the unit cube and the edge skew to it is:
√22
Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (More Than One Correct Option Type Questions)
35 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Statement I And Ii Type Questions)
12 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise For Session 4
10 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
Similar Questions
Find the angle between any two diagonals of a cube.
View SolutionFind the angel between any two diagonals of a cube.
View SolutionProve that the shortest distance between the diagonals of a rectangular parallelopiped whose coterminous sides are a, b, c and the edges not meeting it are
View SolutionKF crystallizes in the rock salt type structure. If the radius of K+ ion is 132 pm and that of F− ion is 135 pm.
(i)What is the shortest distance between K+ and F− ions ?
(ii)What is the edge length of the unit cell ?
(iii)What is closest K-K distance ?
View SolutionThe lengths of two opposite edges of a tetrahedron are a and b; the shortest distane between these edges is d, and the angel between them is θ Prove using vectors that the volume of the tetrahedron is abdsinθ6 .
View SolutionThe length of two opposite edges of a tetrahedron are 12 and 15 units and the shortest distance between them is 10 units. If the volume of the tetrahedron is 200 cubic units, then the angle between the 2 edges is
View SolutionGiven a tetrahedrone D−ABC with AB=12,CD=6. If the shortest distance between the skew lines ABandCD is 8 and angle between them is π6, then find the volume of tetrahedron.
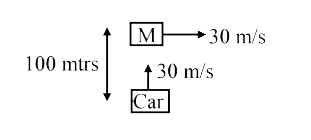
View SolutionThe shortest distance between the car and the motorcycle if their initial positions are as shown, will be :
View SolutionFind the equation of an ellipse the distance between the foci is 8 units and the distance between the directrices is 18 units.
View SolutionThe angle between diagonal of a cube and diagonal
of a face of the cube will be
View Solution
