A silver cylindrical rod has a length of 0.5 m and radius of 0.4 m, find the density of the rod, if its mass is 2640 kg.
To find the density of the silver cylindrical rod, we will follow these steps:
Step 1: Understand the formula for density
The formula for density (ρ) is given by:
ρ=massvolume
Step 2: Identify the given values
From the problem, we have:
- Mass (m) = 2640 kg
- Length (L) = 0.5 m
- Radius (r) = 0.4 m
Step 3: Calculate the volume of the cylinder
The volume (V) of a cylinder is calculated using the formula:
V=πr2L
Substituting the values:
V=π(0.4)2(0.5)
Calculating r2:
(0.4)2=0.16
Now substituting this back into the volume formula:
V=π×0.16×0.5
Calculating 0.16×0.5:
0.16×0.5=0.08
Thus, the volume becomes:
V=π×0.08
Step 4: Substitute the volume into the density formula
Now we substitute the volume back into the density formula:
ρ=2640π×0.08
Step 5: Calculate the value of π
Using the approximate value of π≈3.14:
ρ=26403.14×0.08
Step 6: Calculate 3.14×0.08
Calculating this:
3.14×0.08=0.2512
Step 7: Final calculation for density
Now substituting this value back into the density formula:
ρ=26400.2512
Calculating this gives:
ρ≈10509.55kg/m3
Final Answer
The density of the silver cylindrical rod is approximately:
ρ≈10509.55kg/m3
---
The formula for density (ρ) is given by:
ρ=massvolume
From the problem, we have:
- Mass (m) = 2640 kg
- Length (L) = 0.5 m
- Radius (r) = 0.4 m
The volume (V) of a cylinder is calculated using the formula:
V=πr2L
Substituting the values:
V=π(0.4)2(0.5)
Calculating r2:
(0.4)2=0.16
Now substituting this back into the volume formula:
V=π×0.16×0.5
Calculating 0.16×0.5:
0.16×0.5=0.08
Thus, the volume becomes:
V=π×0.08
Now we substitute the volume back into the density formula:
ρ=2640π×0.08
Using the approximate value of π≈3.14:
ρ=26403.14×0.08
Calculating this:
3.14×0.08=0.2512
Now substituting this value back into the density formula:
ρ=26400.2512
Calculating this gives:
ρ≈10509.55kg/m3
The density of the silver cylindrical rod is approximately:
ρ≈10509.55kg/m3
Topper's Solved these Questions
- PHYSICAL QUANTITIES AND MEASUREMENT BOOK - ICSECHAPTER - PHYSICAL QUANTITIES AND MEASUREMENT EXERCISE - Questions (Choose the correct option to fill in the blank)
4 Videos
- PHYSICAL QUANTITIES AND MEASUREMENT BOOK - ICSECHAPTER - PHYSICAL QUANTITIES AND MEASUREMENT EXERCISE - Exercises (Section I) Name the following
5 Videos
- MODEL TEST PAPERS BOOK - ICSECHAPTER - MODEL TEST PAPERS EXERCISE - Model Test Paper 2 (Section II)
42 Videos
- SOUNDBOOK - ICSECHAPTER - SOUNDEXERCISE - Picture Study
4 Videos
Similar Questions
A solid cylinder of mass 20kg has length 1 m and radius 0.2 m. Then its moment of inertia (in kg-m2) about its geometrical axis is :
View SolutionA cylindrical rod of mass M, length L and radius R has two cords wound around it whose ends are attached to the ceiling. The rod is held horizontally with the two cords vertical. When the rod is released, the cords unwind and the rod rotates the linear acceleration of the cylinder as it falls, is :
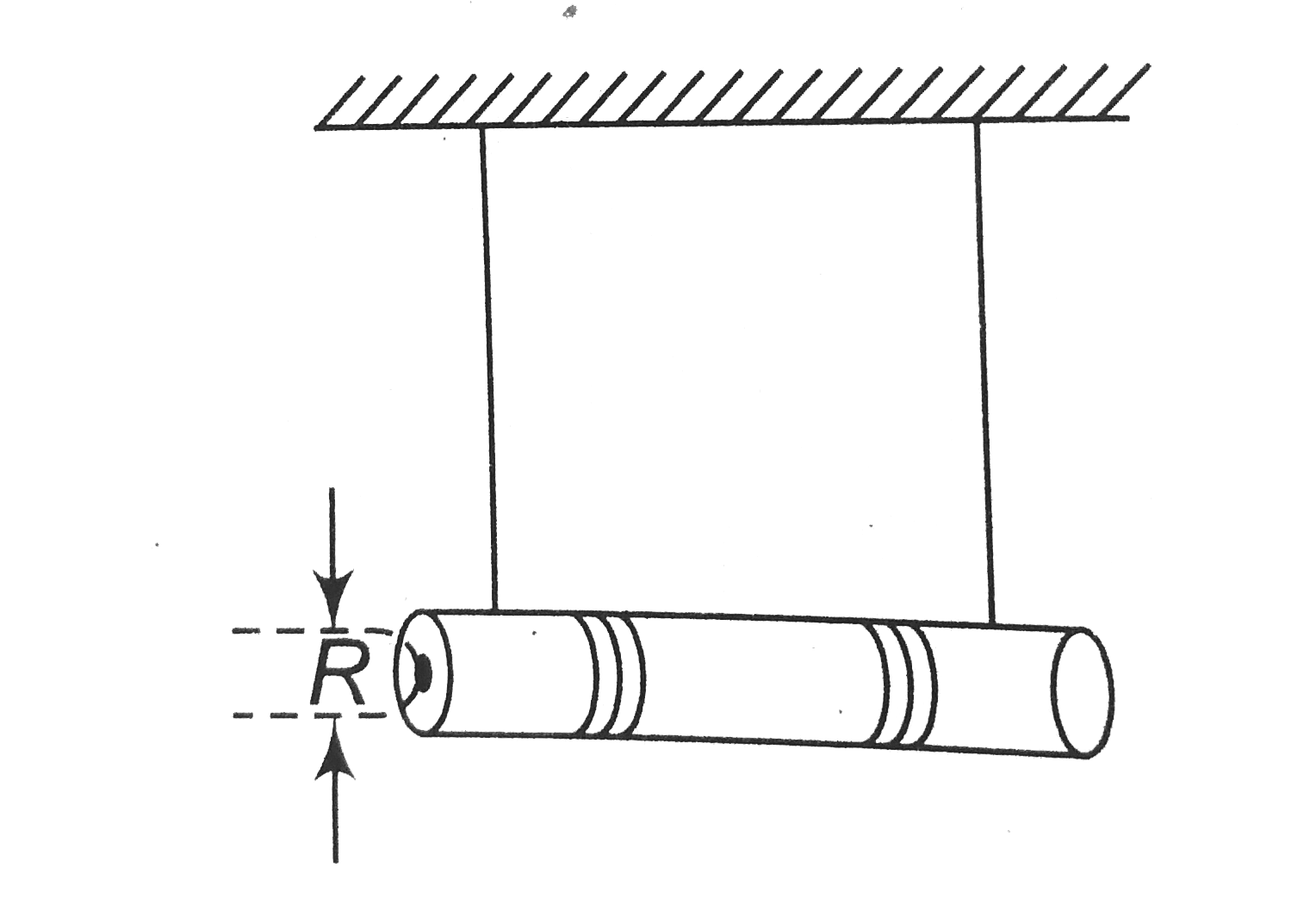 .
.
View SolutionWhen a rod of length 2.5 m and radius 10 mm is subjected to a force the elongation is 3mm and decrease of radius is 0.0025 mm. Find poisson.s ratio of the material of the rod.
View SolutionA sphere has mass of (20±0.4)kg and radius of (10±0.1) m. Find the maximum percentage error in the measurement of density.
View SolutionA rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a speed of v0/4. Find the following: a. The ratio M/m. b. The angular velocity of the rod about O. c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
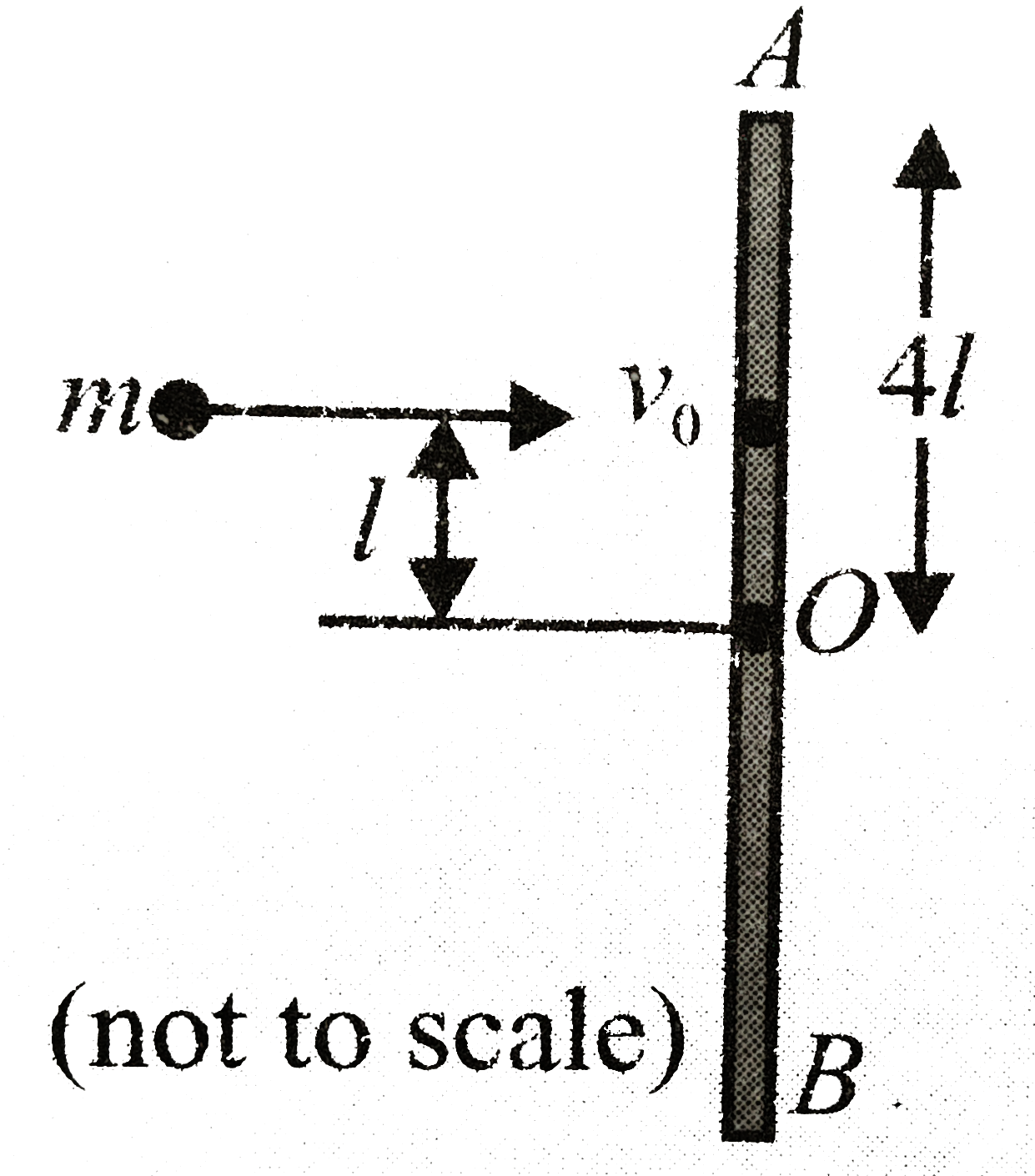
View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionFind the moment of inertia A of a spherical ball of mass m and radius r attached at the end of a straight rod of mass M and length l, if this system is free to rotate about an axis passing through the end of the rod (end of the rod opposite to sphere).

View SolutionThe curved surface area of a cylindrical rod is 132 cm2. Find its length if the radius is 0.35cm.
View SolutionA non-uniform rod AB has a mass M ad length 2l. The mass per unit length of the rod is mx at a point of the rod distant x from A. find the moment of inertia of this rod about an axis perpendicular to the rod (a) through A (b) through the mid-point of AB.
View SolutionA physical pendulum shown in Fig. is made up of a rod 60 cm long with mass 0.50 kg and a disk of 3.0 cm radius with mass 0.60 kg. Find the period of this pendulum.

View Solution
