Solve any two sub questions from the following :
There are trees on both the sides of a straight road. The distance between consecutive trees is 11.2 m. If the road is 2 km 800 m long, how many trees are there on the road ?
To solve the problem step by step, we will calculate the number of trees on both sides of the road given the distance between consecutive trees and the total length of the road.
Step 1: Convert the length of the road to meters
The length of the road is given as 2 km 800 m. We need to convert this into meters for easier calculations.
- 1 km = 1000 m
- Therefore, 2 km = 2 × 1000 m = 2000 m
- Adding the remaining 800 m gives us:
Total length in meters=2000m+800m=2800m
Step 2: Calculate the number of gaps between trees on one side of the road
The distance between consecutive trees is 11.2 m. To find the number of gaps (which is one less than the number of trees), we divide the total length of the road by the distance between the trees:
Number of gaps=Total lengthDistance between trees=2800m11.2m
Calculating this gives:
Number of gaps=250
Step 3: Calculate the number of trees on one side of the road
Since the number of trees is one more than the number of gaps, we add 1 to the number of gaps:
Number of trees on one side=Number of gaps+1=250+1=251
Step 4: Calculate the total number of trees on both sides of the road
Since there are trees on both sides of the road, we multiply the number of trees on one side by 2:
Total number of trees=251×2=502
Final Answer
The total number of trees on both sides of the road is 502.
---
The length of the road is given as 2 km 800 m. We need to convert this into meters for easier calculations.
- Therefore, 2 km = 2 × 1000 m = 2000 m
- Adding the remaining 800 m gives us:
Total length in meters=2000m+800m=2800m
The distance between consecutive trees is 11.2 m. To find the number of gaps (which is one less than the number of trees), we divide the total length of the road by the distance between the trees:
Since the number of trees is one more than the number of gaps, we add 1 to the number of gaps:
Since there are trees on both sides of the road, we multiply the number of trees on one side by 2:
The total number of trees on both sides of the road is 502.
Topper's Solved these Questions
Similar Questions
Solve any two sub questions from the following :
Solve any two of the following equations :
19=m−4
View SolutionOn a 2 km road, a total number of 201 trees are planted on each side of the road at equal distances. How many such trees in all will be planted on both sides of a 50 km road such that the distance between two consecutive trees is the same as that of the consecutive trees on the 2 km road? (a) 501 (b) 5000 (c) 5001 (d) 5025 (e) 5050
View Solution
Knowledge Check
In a row, 25 trees are planted at equal distance from each other. The distance between 1st and 25th tree is 30m. What is the distance between 3rd and 15th tree?
A8 mB15 mC16 mD18 mIn a row, 25 trees are planted at equal distance from each other. The distance between 1st and 25th tree is 30m. What is the distance between 3rd and 15th tree?
A8 mB15 mC16 mD18 mA tree Ac is broken over by wind from B . D is the point where the top of the broken tree touches the ground and BD makes an angle of 45∘ with the ground . If the distance between the base of the tree and the point D = 10 m What is the height of the tree ?
A20√3mB60 mC20(√3−1)mD40√3m
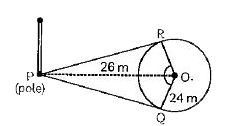
If six trees are to be planted along each tangential line segments at equal distances, find the distance between any two consecutive trees.
View SolutionA road is 4km 800m long.If trees are planted on both its sides at intervals of 9.6 how many trees were planted?
View SolutionTwo towns A and B are situated on the same side of a straight road at distances a and brespectively perpendiculars drawn from A and B meet the road at point C and D respectively.The distance between C and D is c. A hospital is to be built at a point P on the road such thatthe distance APB is minimum. Find position of P.
View SolutionFind the maximum number of trees which can be planted, 20 metres apart, on the two sides of a straight road 1760 metres long
View SolutionFind the maximum number of trees which can be planted, 20 metres apart, on the two sides of a straight road 1760 metres long
View Solution
