In a parallelogram ABCD, AB= 20 cm and AD= 12cm. The bisector of angle A meets DC at E and BC produced at F. Find the length of CF.
The correct Answer is:8cm
To solve the problem step by step, we will use the properties of a parallelogram and the angle bisector theorem.
1. Draw the Parallelogram:
- Start by drawing parallelogram ABCD where AB = 20 cm and AD = 12 cm.
- Since opposite sides of a parallelogram are equal, we have BC = 20 cm and DC = 12 cm.
2. Identify the Points:
- Mark the points A, B, C, and D accordingly.
- Let the angle bisector of angle A meet side DC at point E and the extended line of BC at point F.
3. Assume the Length CF:
- Let CF = x cm.
- Therefore, BC (which is equal to AD) can be expressed as BC = 12 cm + CF = 12 cm + x.
4. Use the Angle Bisector Theorem:
- According to the angle bisector theorem, the ratio of the lengths of the two segments created by the angle bisector is equal to the ratio of the other two sides of the triangle.
- In triangle ABF, the angle bisector divides BF into segments BE and EF such that:
ABAF=BEEF
- Here, AB = 20 cm and AF = BC = 12 cm + x.
5. Set Up the Equation:
- Since BE is equal to BC (12 cm) and EF is equal to CF (x), we can write:
2012+x=12x
6. Cross-Multiply:
- Cross-multiplying gives:
20x=12(12+x)
7. Expand and Simplify:
- Expanding the right side:
20x=144+12x
- Rearranging gives:
20x−12x=144
8x=144
8. Solve for x:
- Dividing both sides by 8:
x=1448=18
9. Conclusion:
- Therefore, the length of CF is 18 cm.
Final Answer:
CF = 18 cm
- Start by drawing parallelogram ABCD where AB = 20 cm and AD = 12 cm.
- Since opposite sides of a parallelogram are equal, we have BC = 20 cm and DC = 12 cm.
- Mark the points A, B, C, and D accordingly.
- Let the angle bisector of angle A meet side DC at point E and the extended line of BC at point F.
- Let CF = x cm.
- Therefore, BC (which is equal to AD) can be expressed as BC = 12 cm + CF = 12 cm + x.
- According to the angle bisector theorem, the ratio of the lengths of the two segments created by the angle bisector is equal to the ratio of the other two sides of the triangle.
- In triangle ABF, the angle bisector divides BF into segments BE and EF such that:
ABAF=BEEF
- Here, AB = 20 cm and AF = BC = 12 cm + x.
- Since BE is equal to BC (12 cm) and EF is equal to CF (x), we can write:
2012+x=12x
- Cross-multiplying gives:
20x=12(12+x)
- Expanding the right side:
20x=144+12x
- Rearranging gives:
20x−12x=144
8x=144
- Dividing both sides by 8:
x=1448=18
- Therefore, the length of CF is 18 cm.
CF = 18 cm
Topper's Solved these Questions
- BOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - Exercise 14(C )28videos
RECTILINEAR FIGURES
- BOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - POLYGONS - 3 MARKS QUESTIONS5videos
RECTILINEAR FIGURES
- BOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - Exercise 14(B) (true/false)10videos
RECTILINEAR FIGURES
- BOOK - ICSECHAPTER - RATIONAL AND IRRATIONAL NUMBERS EXERCISE - EXERCISE 1 (D)21videos
RATIONAL AND IRRATIONAL NUMBERS
- BOOK - ICSECHAPTER - SIMULTANEOUS EQUATIONSEXERCISE - EXERCISE 6 (G)13videos
SIMULTANEOUS EQUATIONS
Similar Questions
In a parallelogram ABCD, AB = 10 cm and AD = 6 cm. The bisector of ∠A meets DC in E. AE and BC produced meet at F. Find the length of CF.
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2AD. Prove that:
Angle APB= 90∘View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2AD. Prove that:
BP bisects angle BView SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB = 2AD.
Prove that :
(i) BP bisects angle B.
(ii) Angle APB = 90∘View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
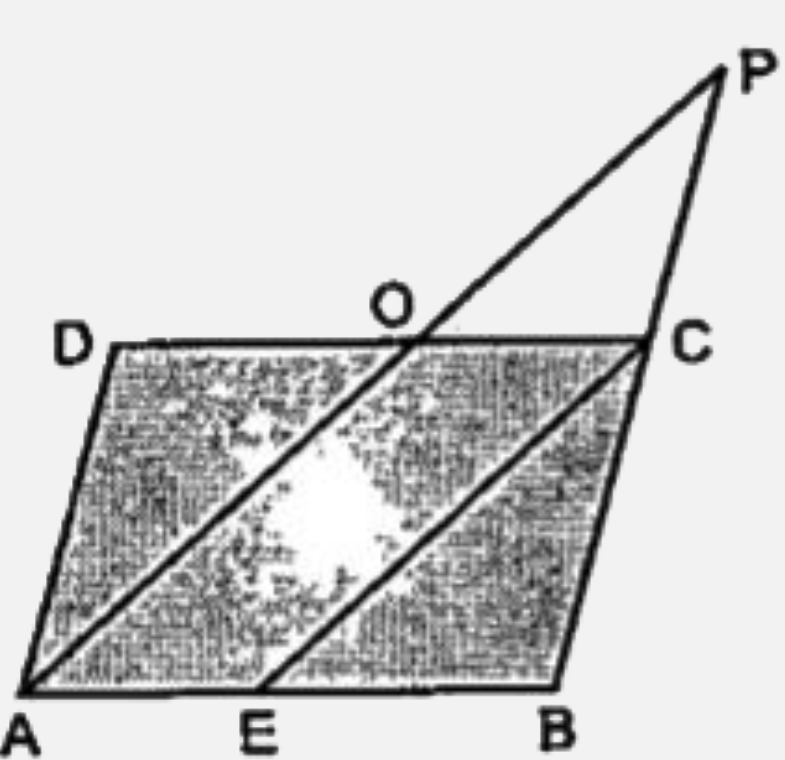
BP=2ADView SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
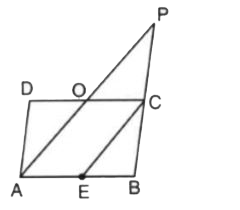
PB=2ADView SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:

O is mid-point of AP.View SolutionIn a triangle ABC , AB = AC and ∠A=36∘ If the internal bisector of angle C meets AB at D . Prove that AD = BC.
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View SolutionIn the following figure , ABCD is a cyclic quadrilateral in which AD is parallel to BC .
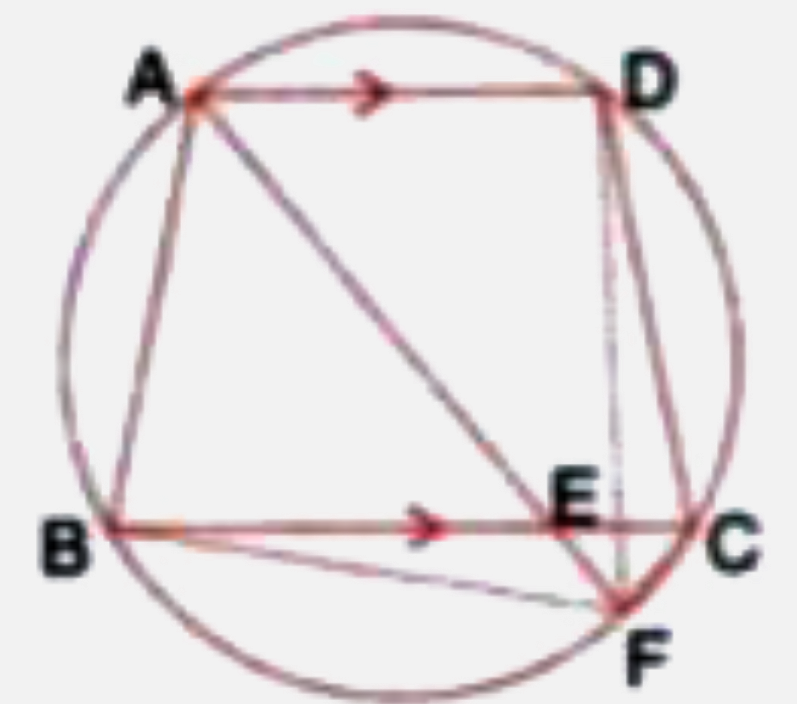
If the bisector of angle A meets BC at point E and given circle at point F, prove that :
(i) EF =FC
(ii) BF = DFView Solution

