In parallelogram ABCD, the bisector of angle A meets DC at P and AB = 2AD.
Prove that :
(i) BP bisects angle B.
(ii) Angle APB = 90∘
To solve the problem step by step, we will follow the reasoning presented in the video transcript.
Given:
- Parallelogram ABCD
- Angle bisector of angle A meets DC at point P
- AB = 2AD
To Prove:
1. BP bisects angle B.
2. Angle APB = 90°.
Step 1: Draw the Parallelogram
Draw parallelogram ABCD with points A, B, C, and D labeled in a clockwise manner. Mark point P where the angle bisector of angle A meets line DC.
Step 2: Identify Angles
Let angle A be divided into two equal angles, each denoted as θ. Therefore, angle PAB = θ and angle DAP = θ.
Step 3: Use Properties of Parallelogram
Since ABCD is a parallelogram, we know that:
- AB is parallel to CD
- AD is parallel to BC
Step 4: Establish Relationships
From the properties of parallel lines cut by a transversal (AP), we have:
- Angle PAB = Angle APD (alternate interior angles)
- Therefore, angle APD = θ.
Step 5: Isosceles Triangle
Since angle PAB = angle APD, triangle ADP is isosceles. Hence, AD = PD.
Step 6: Relate Sides
Given that AB = 2AD, we can express CD as:
- CD = AB = 2AD.
Step 7: Express CD in Terms of PD
Since CD = PD + PC, we can write:
- 2AD = PD + PC.
Step 8: Substitute PD
Since PD = AD, we substitute:
- 2AD = AD + PC,
- Therefore, PC = AD.
Step 9: Establish Equality
Now we have:
- AD = PD = PC.
Step 10: Prove Triangle PBC is Isosceles
Since AD = PC, triangle PBC is also isosceles:
- PB = PC.
Step 11: Angles in Isosceles Triangle
In triangle PBC, since PB = PC, we have:
- Angle CPB = Angle PBC (base angles of an isosceles triangle).
Step 12: Relate Angles B
Since AB is parallel to CD and PB is a transversal, we have:
- Angle CPB = Angle PBA (alternate interior angles).
Step 13: Conclude BP Bisects Angle B
Thus, we conclude that:
- BP bisects angle B.
Step 14: Prove Angle APB = 90°
Now, we need to show that angle APB = 90°.
Step 15: Use Triangle Sum Property
In triangle APB, we know:
- Angle PAB = θ,
- Angle PBA = φ (where φ = angle CPB).
Step 16: Establish Relationships
From earlier, we established:
- Angle A = 2θ,
- Angle B = 2φ.
Step 17: Use Sum of Angles in Parallelogram
Since A + B = 180° (adjacent angles in a parallelogram):
- 2θ + 2φ = 180°,
- θ + φ = 90°.
Step 18: Substitute Values
Since we established that θ = φ (from isosceles triangle properties):
- 2θ = 90°,
- Therefore, θ = 45°.
Step 19: Conclude Angle APB
Using the triangle sum property in triangle APB:
- Angle PAB + Angle APB + Angle PBA = 180°,
- θ + Angle APB + θ = 180°,
- 2θ + Angle APB = 180°,
- Angle APB = 180° - 90° = 90°.
Conclusion
Thus, we have proved both parts:
1. BP bisects angle B.
2. Angle APB = 90°.
- Parallelogram ABCD
- Angle bisector of angle A meets DC at point P
- AB = 2AD
1. BP bisects angle B.
2. Angle APB = 90°.
Draw parallelogram ABCD with points A, B, C, and D labeled in a clockwise manner. Mark point P where the angle bisector of angle A meets line DC.
Let angle A be divided into two equal angles, each denoted as θ. Therefore, angle PAB = θ and angle DAP = θ.
Since ABCD is a parallelogram, we know that:
- AB is parallel to CD
- AD is parallel to BC
From the properties of parallel lines cut by a transversal (AP), we have:
- Angle PAB = Angle APD (alternate interior angles)
- Therefore, angle APD = θ.
Since angle PAB = angle APD, triangle ADP is isosceles. Hence, AD = PD.
Given that AB = 2AD, we can express CD as:
- CD = AB = 2AD.
Since CD = PD + PC, we can write:
- 2AD = PD + PC.
Since PD = AD, we substitute:
- 2AD = AD + PC,
- Therefore, PC = AD.
Now we have:
- AD = PD = PC.
Since AD = PC, triangle PBC is also isosceles:
- PB = PC.
In triangle PBC, since PB = PC, we have:
- Angle CPB = Angle PBC (base angles of an isosceles triangle).
Since AB is parallel to CD and PB is a transversal, we have:
- Angle CPB = Angle PBA (alternate interior angles).
Thus, we conclude that:
- BP bisects angle B.
Now, we need to show that angle APB = 90°.
In triangle APB, we know:
- Angle PAB = θ,
- Angle PBA = φ (where φ = angle CPB).
From earlier, we established:
- Angle A = 2θ,
- Angle B = 2φ.
Since A + B = 180° (adjacent angles in a parallelogram):
- 2θ + 2φ = 180°,
- θ + φ = 90°.
Since we established that θ = φ (from isosceles triangle properties):
- 2θ = 90°,
- Therefore, θ = 45°.
Using the triangle sum property in triangle APB:
- Angle PAB + Angle APB + Angle PBA = 180°,
- θ + Angle APB + θ = 180°,
- 2θ + Angle APB = 180°,
- Angle APB = 180° - 90° = 90°.
Thus, we have proved both parts:
1. BP bisects angle B.
2. Angle APB = 90°.
Topper's Solved these Questions
- RECTILINEAR FIGURESBOOK - ICSECHAPTER - RECTILINEAR FIGURESEXERCISE - QUADRILATERALS AND ITS PROPERTIES - 3 MARKS QUESTIONS
8 Videos
- RATIONAL AND IRRATIONAL NUMBERS BOOK - ICSECHAPTER - RATIONAL AND IRRATIONAL NUMBERS EXERCISE - EXERCISE 1 (D)
21 Videos
- SIMULTANEOUS EQUATIONSBOOK - ICSECHAPTER - SIMULTANEOUS EQUATIONSEXERCISE - EXERCISE 6 (G)
13 Videos
Similar Questions
In parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2AD. Prove that:
BP bisects angle B
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2AD. Prove that:
Angle APB= 90∘
View SolutionIn a parallelogram ABCD, the bisector of ∠A bisects the line B at point X. Prove that AD = 2AB.
View SolutionIn parallelogram ABCD, E is the mid-point of side AB and CE bisect angle BCD. Prove that :
(i) AE=AD
(ii) DE bisect ∠ADC and
(iii) Angle DEC is a right angle.
View SolutionIn a parallelogram ABCD, AB= 20 cm and AD= 12cm. The bisector of angle A meets DC at E and BC produced at F. Find the length of CF.
View SolutionIn a quadrilateral ABCD, AB= AD and CB= CD. Prove that:
AC bisects angle BAD
View SolutionIn the following figure , ABCD is a cyclic quadrilateral in which AD is parallel to BC .
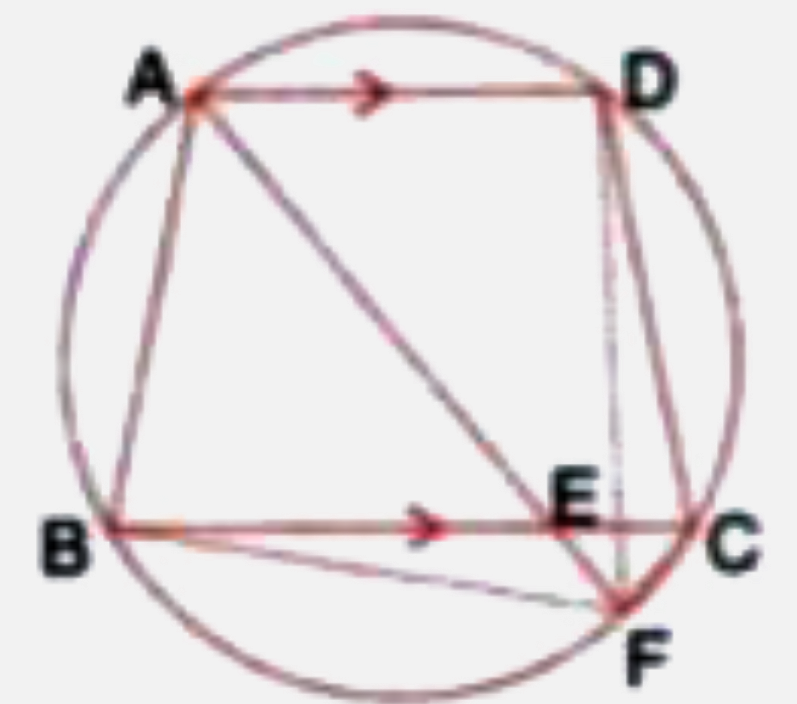
If the bisector of angle A meets BC at point E and given circle at point F, prove that :
(i) EF =FC
(ii) BF = DF
View SolutionIn parallelogram ABCD, the bisectors of adjacent angles A and D intersect each other at point P. prove that ∠APD=90∘.
View SolutionIn ΔABC, AB = AC and the bisectors of angles B and C intersect at point O. Prove that :
(i) BO = CO
(ii) AO bisects angle BAC.
View SolutionIn quadrilateral ABCD, AD = BC and BD = CA. Prove that :
(i) ∠ADB=∠BCA
(ii) ∠DAB=∠CBA
View Solution
