In the given figure, a square is inscribed in a circle with centre O. Find :
∠COD . Is BD a diameter of the circle
To solve the problem step by step, we will analyze the given figure and apply the properties of a square and a circle.
1. Understanding the Figure:
- We have a square inscribed in a circle with center O. Let's label the vertices of the square as A, B, C, and D in clockwise order. The diagonals of the square are AC and BD.
2. Identifying the Angles:
- The diagonals of a square intersect at right angles (90 degrees). Therefore, angle AOB (formed by the diagonal AC and line OB) and angle COD (formed by the diagonal BD and line OC) are both right angles.
3. Finding angle COD:
- Since the diagonals of the square intersect at right angles, we have:
∠COD=90∘
4. Checking if BD is a Diameter:
- Since angle BOC + angle COD = 180 degrees (because they are on a straight line BD), and we already established that angle COD = 90 degrees, it follows that:
∠BOC=180∘−∠COD=180∘−90∘=90∘
- This means that angle BOC is also a right angle, confirming that points B and D lie on the circle and that BD is indeed a diameter of the circle.
5. Conclusion:
- Therefore, we conclude that:
- ∠COD=90∘
- Yes, BD is a diameter of the circle.
- We have a square inscribed in a circle with center O. Let's label the vertices of the square as A, B, C, and D in clockwise order. The diagonals of the square are AC and BD.
- The diagonals of a square intersect at right angles (90 degrees). Therefore, angle AOB (formed by the diagonal AC and line OB) and angle COD (formed by the diagonal BD and line OC) are both right angles.
- Since the diagonals of the square intersect at right angles, we have:
∠COD=90∘
- Since angle BOC + angle COD = 180 degrees (because they are on a straight line BD), and we already established that angle COD = 90 degrees, it follows that:
∠BOC=180∘−∠COD=180∘−90∘=90∘
- This means that angle BOC is also a right angle, confirming that points B and D lie on the circle and that BD is indeed a diameter of the circle.
- Therefore, we conclude that:
- ∠COD=90∘
- Yes, BD is a diameter of the circle.
Topper's Solved these Questions
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)
12 Videos
- CIRCLEBOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(B)
15 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
- CIRCLES BOOK - ICSECHAPTER - CIRCLES EXERCISE - TOPIC-2
25 Videos
Similar Questions
In the given figure, a square is inscribed in a circle with centre O. Find :
∠BOD .Is BD a diameter of the circle
View SolutionIn the given figure, a square is inscribed in a circle with centre O. Find :
∠BOC . Is BD a diameter of the circle
View SolutionIn the given figure, a square is inscribed in a circle with centre O. Find :
∠OCB . Is BD a diameter of the circle
View SolutionIn the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
∠OBC
View SolutionIn the given figure, an equilateral triangle ABC is inscribed in a circle with centre O. Find :
∠BOC
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
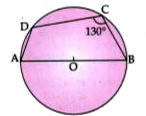
∠BCD=130∘. Find
(i) ∠DAB
View SolutionIn the given figure, AB is the diameter of a circle with centre O.
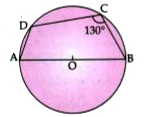
∠BCD=130∘. Find
(ii) ∠DBA
View SolutionA square is inscribed in a circle of radius 7 cm. Find the area of the square.
View SolutionIn figure, a square is inscribed in a circle of diameter d and another square is circumscribing the circle . Is the area of the outer square four times the area of the inner square ? Give reason for your answer.

View SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
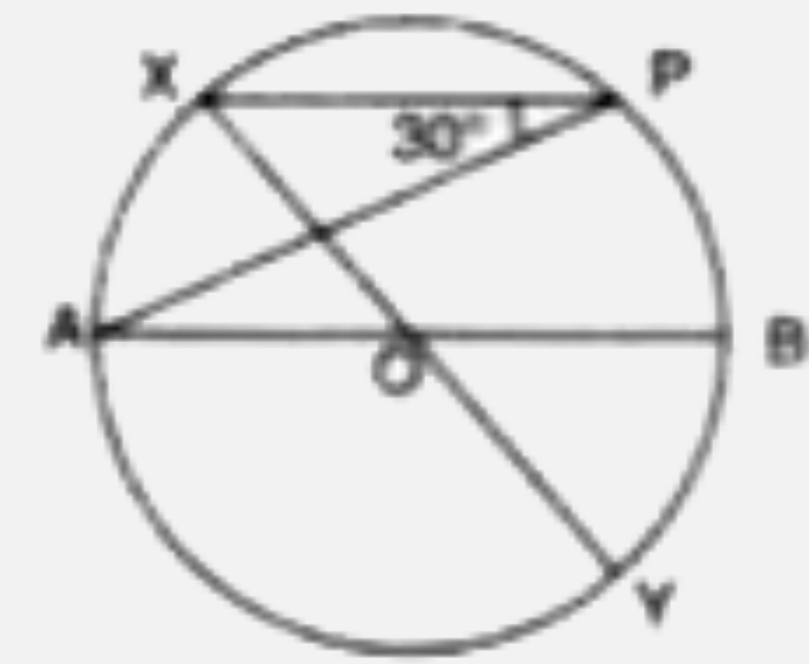
∠BPY
View Solution
