In the given figure, arc AB and arc BC are equal in length. If ∠AOB=48∘, find
∠OAC
Step by step video & image solution for In the given figure, arc AB and arc BC are equal in length. If angleAOB = 48^(@), find angleOAC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(D)12videos
CIRCLE
- BOOK - ICSECHAPTER - CIRCLEEXERCISE - EXERCISE 17(B)15videos
CIRCLE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA11videos
CHAPTERWISE REVISION (STAGE 3)
- BOOK - ICSECHAPTER - CIRCLES EXERCISE - TOPIC-225videos
CIRCLES
Similar Questions
In the given the length of arcs AB and BC are in the ratio 3:2.
If ∠AOB=96∘ find
∠ABCView SolutionIn the given the length of arcs AB and BC are in the ratio 3:2.
If ∠AOB=96∘ find
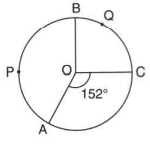
∠BOCView SolutionIn the given figure, lengths of arcs APB and BQC are in the ratio 5:3 and angle AOC=152∘, find angle ACB and angle BAC.
View SolutionIn the given figure , the lengths of arc AB and are BC arc in the ratio 3: 2 if ∠AOB=96∘, find
(i)∠CAB(ii)∠ADB
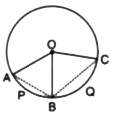
View SolutionIn the given figure , arc APB : arc BQC = 2: 3 and ∠AOC=150∘, Find :
(i) ∠AOB
(ii) ∠BOC
(iii) ∠OBA
(iv) ∠OCB
(v) ∠ABC
View SolutionIn the given figure AB, BC, BD cannot be in
View SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
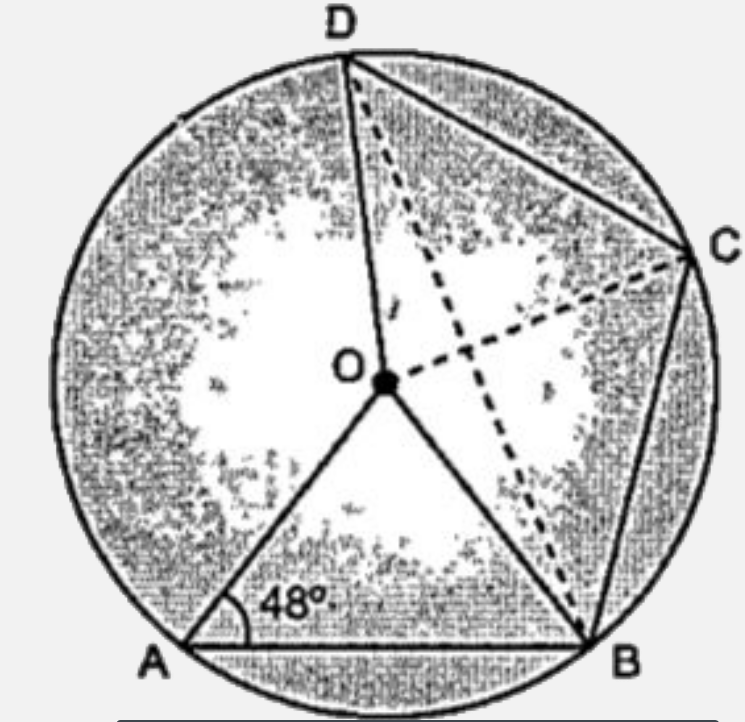
∠OBDView SolutionIn the given figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC.
if ∠AOB=100∘ find ∠BOCView SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠OACView SolutionIn the given arc AB= twice are BC and ∠AOB=80∘ find:
∠BOCView Solution